Advertisements
Advertisements
प्रश्न
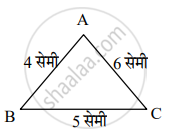
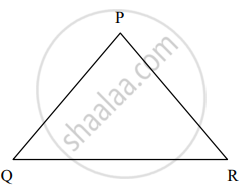
दोन समरूप त्रिकोणांपैकी लहान त्रिकोणाच्या बाजू 4 सेमी, 5 सेमी, 6 सेमी लांबीच्या आहेत आणि मोठ्या त्रिकोणाची परिमिती 90 सेमी आहे, तर मोठ्या त्रिकोणाच्या बाजू काढा.
उत्तर
पक्ष: ∆ABC ~ ∆PQR
∆ABC मध्ये, AB = 4 सेमी, BC = 5 सेमी, AC = 6 सेमी
∆PQR मध्ये, PQ + QR + PR = 90 सेमी
शोधा: PQ, QR आणि PR
उकल:
∆ABC ~ ∆PQR …[पक्ष]
∴ `"AB"/"PQ" = "BC"/"QR" = "AC"/"PR"` = …[समरूप त्रिकोणांच्या संगत बाजू]
समजा, `"AB"/"PQ" = "BC"/"QR" = "AC"/"PR"` = k
∴ `4/"pQ" = 5/"QR" = 6/"PR" = "k"` .....[पक्ष]
∴ `4/"PQ" = "k", 5/"QR" = "k"` आणि `6/"PR" = "k"`
∴ PQ = `4/"k", "QR" = 5/"k"` आणि PR = `6/"k"` ...(i)
∴ PQ + QR + PR = `4/"k" + 5/"k" + 6/"k"`
∴ 90 = `15/"k"` ..............[पक्ष]
∴ k = `15/90`
= `1/6`
∴ PQ = `4/((1/6))` = 4 × 6 = 24 सेमी .........[(i) वरून]
∴ QR = `5/((1/6))` = 5 × 6 = 30 सेमी .........[(i) वरून]
∴ PR = `6/((1/6))` = 6 × 6 = 36 सेमी .........[(i) वरून]
∴ मोठ्या त्रिकोणाच्या बाजू 24 सेमी, 30 सेमी आणि 36 सेमी आहेत.
APPEARS IN
संबंधित प्रश्न
दोन समरूप त्रिकोणांच्या संगत बाजूंचे गुणोत्तर 3 : 5 आहे, तर त्यांच्या क्षेत्रफळांचे गुणोत्तर काढा.
ΔABC ∼ ΔPQR आणि AB : PQ = 2 : 3, तर खालील चौकटी पूर्ण करा.
`("A"(Δ"ABC"))/("A"(Δ"PQR")) = ("AB"^2)/square" = 2^2/3^2 = square/square`
ΔABC व ΔDEF मध्ये ∠B = ∠E, ∠F = ∠C आणि AB = 3 DE, तर त्या दोन त्रिकोणांबाबत सत्य विधान कोणते?
जर ΔABC ~ ΔPQR आणि AB : PQ = 3:4, तर A(ΔABC) : A(ΔPQR) किती?
जर ∆ABC ~ ∆LMN आणि ∠A = 60° असल्यास ∠L = ?
∆ABC मध्ये, AP लंब BC व BQ लंब AC, B-P-C, A-Q-C, तर ∆CPA ~ ∆CQB दाखवा. जर AP = 7, BQ = 8, BC = 12 असल्यास AC ची किंमत काढा.
∆CPA व ∆CQB मध्ये,
∠CPA ≅ `square` ...........[प्रत्येकी 90°]
∠ACP ≅ `square` ...........[सामाईक कोन]
∆CPA ~ ∆CQB ............[`square` समरूपता कसोटी]
`"AP"/"BQ" = square/"BC"` ............…[समरूप त्रिकोणांच्या संगत बाजू प्रमाणात]
`7/8 = square/12`
AC × `square` = 7 × 12
AC = 10.5
समभुज त्रिकोण PQR ची बाजू 8 सेमी आहे, तर त्या त्रिकोणाच्या बाजूपेक्षा निम्म्या बाजू असणाऱ्या समभुज त्रिकोणाचे क्षेत्रफळ काढा.
दोन समरूप त्रिकोणांची क्षेत्रफळे समान असल्यास ते त्रिकोण एकरूप असतात. सिद्ध करा.
जर ΔABC ∼ ΔPQR आणि `("A"(Delta"ABC"))/(A(Delta"PQR")) = 16/25` तर AB : PQ किती?
ΔABC मध्ये रेख DE || बाजू BC. जर 2A(ΔADE) = A(⬜ DBCE), तर AB : AD आणि BC = `sqrt3` DE दाखवा.
