Advertisements
Advertisements
प्रश्न
Draw a circle of diameter 9 cm. Mark a point at a distance of 7.5 cm from the centre of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
उत्तर
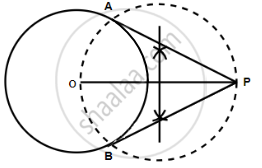
Steps of construction:
- Draw a circle of diameter 9 cm, taking O as the centre.
- Mark a point P outside the circle, such that PO = 7.5 cm.
- Taking OP as the diameter, draw a circle such that it cuts the earlier circle at A and B.
- Join PA and PB.
APPEARS IN
संबंधित प्रश्न
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :
- A circle of radius 2.5 cm, passing through A and C.
- Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
Draw a circle of radius 4.2. Draw a pair of tangents to this circle inclined to each other at an angle of 45°
Draw a circle of radius 32 cm. Draw a tangent to the circle making an angle 30° with a line passing through the centre.
Draw a circle of radius 3 cm. Construct a square about the circle.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 60°, it is required to draw tangents at end points of those two radii of the circle, the angle between them should be ______.
A pair of tangents can be constructed from a point P to a circle of radius 3.5cm situated at a distance of ______ from the centre.
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
Draw a circle of radius 2.5 cm. Construct a pair of tangents from a point Pat a distance of 6 cm from the centre of the circle.
