Advertisements
Advertisements
प्रश्न
Draw ∠ABC of measures 135°and bisect it.
उत्तर १
Steps of Construction:
1. Draw a line of convenient length. Take a point B on it. With B as centre, draw an arc that cuts the line at points X and Y.
2. With X as centre, cut an arc at P on the previous arc.
3. With P as centre and same radius in the compass, cut another arc at Q.
4. With P and Q as centres, cut intersecting arcs and name it as point E. Join EB.
5. With O and Y as centres, draw intersecting arcs and name the intersection point A. Join AB.
Here, ∠ABC is the required angle of measure 135°.
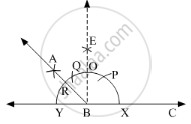
With R and X as centres, form intersecting arcs which meet at point G.
Here, BG is the required bisector of ∠ABC.
उत्तर २
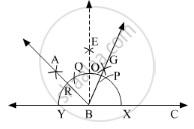
Steps of Construction:
1. Draw a line of convenient length. Take a point B on it. With B as centre, draw an arc that cuts the line at points X and Y.
2. With X as centre, cut an arc at P on the previous arc.
3. With P as centre and same radius in the compass, cut another arc at Q.
4. With P and Q as centres, cut intersecting arcs and name it as point E. Join EB.
5. With O and Y as centres, draw intersecting arcs and name the intersection point A. Join AB.
Here, ∠ABC is the required angle of measure 135°.

With R and X as centres, form intersecting arcs which meet at point G.
Here, BG is the required bisector of ∠ABC.

APPEARS IN
संबंधित प्रश्न
ΔSHR ~ ΔSVU. In ΔSHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and `"SH"/("SV")=3/5`. Construct ΔSVU.
Draw ∠ABC of measure 105° and bisect it.
Draw `angle ABC` of measure 80° and bisect it
Ponit M is the mid point of seg AB and AB = 14 then AM = ?
If Δ ABC ∼ Δ XYZ then complete the following brackets.
`(AB)/(XY) = /(YZ) = (AC)/`
Draw ∠ ARP= 115° and bisect it.
Write down the equation of X- axis.
Draw seg AB of length 5.7 cm and bisect it.
Prove that “That ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.”
Construct ∠ABC = 60° and bisect it
Construct ∠PQR = 115° and divide it into two equal parts
Draw seg AB of length 4.5 cm and draw its perpendicular bisector
Point P is at a distance of 6 cm from line AB. Draw a circle of radius 4 cm passing through point P so that line AB is the tangent to the circle
