Advertisements
Advertisements
Question
Draw ∠ABC of measures 135°and bisect it.
Solution 1
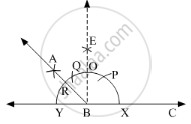
Steps of Construction:
1. Draw a line of convenient length. Take a point B on it. With B as centre, draw an arc that cuts the line at points X and Y.
2. With X as centre, cut an arc at P on the previous arc.
3. With P as centre and same radius in the compass, cut another arc at Q.
4. With P and Q as centres, cut intersecting arcs and name it as point E. Join EB.
5. With O and Y as centres, draw intersecting arcs and name the intersection point A. Join AB.
Here, ∠ABC is the required angle of measure 135°.
With R and X as centres, form intersecting arcs which meet at point G.
Here, BG is the required bisector of ∠ABC.
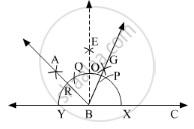
Solution 2
Steps of Construction:
1. Draw a line of convenient length. Take a point B on it. With B as centre, draw an arc that cuts the line at points X and Y.
2. With X as centre, cut an arc at P on the previous arc.
3. With P as centre and same radius in the compass, cut another arc at Q.
4. With P and Q as centres, cut intersecting arcs and name it as point E. Join EB.
5. With O and Y as centres, draw intersecting arcs and name the intersection point A. Join AB.
Here, ∠ABC is the required angle of measure 135°.

With R and X as centres, form intersecting arcs which meet at point G.
Here, BG is the required bisector of ∠ABC.

APPEARS IN
RELATED QUESTIONS
ΔSHR ~ ΔSVU. In ΔSHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and `"SH"/("SV")=3/5`. Construct ΔSVU.
Draw ∠ABC of measure 105° and bisect it.
Draw `angle ABC` of measure 80° and bisect it

Observe the adjoining figure and write down one pair of interior angles.
If Δ ABC ∼ Δ XYZ then complete the following brackets.
`(AB)/(XY) = /(YZ) = (AC)/`
Draw ∠ ARP= 115° and bisect it.
Write down the equation of X- axis.
Draw seg AB of length 5.7 cm and bisect it.
Draw ∠ABC of measure 120° and bisect it.
Prove that “That ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.”
Construct ∠ABC = 60° and bisect it
Construct ∠PQR = 115° and divide it into two equal parts
Draw Seg AB of length 9.7 cm. Take point P on it such that AP = 3.5 cm and A–P–B. Construct perpendicular to seg AB from point P.
Draw seg AB of length 4.5 cm and draw its perpendicular bisector
