Advertisements
Advertisements
प्रश्न
Draw the circle with centre C and radius 3.5 cm. Point B is at a distance 7 cm from the centre. Draw tangents to the circle from the point B.
उत्तर
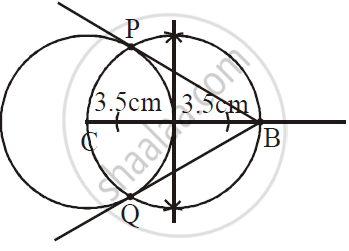
1) Take centre C
2) Draw circle of radius 3.5 cm
3) Extend CA till CB where l(CB) = 7cm
4) Take distance more than half in compass and mark two arcs from the ends to line CB.
5) Now draw two more arcs above and below the line keeping the compass on these arcs.
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 3.5 cm. Take any point K on it. Draw a tangent to the circle at K without using centre of the circle.
Draw a tangent at any point ‘P’ on the circle of radius 3.5 cm and centre O.
Draw a circle of radius 3.6 cm. Draw a tangent to the circle at any point on it without using the centre.
Select the correct alternative for the following question.
The maximum number of tangents that can be drawn to a circle from a point out side it is .............. .
Draw a circle with centre O and radius 3.5 cm. Take point P at a distance 5.7 cm from the centre. Draw tangents to the circle from point P.
Choose the correct alternative:
______ number of tangents can be drawn to a circle from the point outside the circle
| Draw a circle and take any point P on the circle. Draw ray OP |
| ↓ |
| Draw perpendicular to ray OP from point P |
To draw tangents to the circle from the endpoints of the diameter of the circle.
| Construct a circle with center O. Draw any diameter AB of it |
| ↓ |
| Draw ray OA and ray OB |
| ↓ |
| Construct perpendicular to ray OA from point A |
| ↓ |
| Construct perpendicular to Ray OB from point B |
Draw a circle of radius 4.2 cm. Draw a tangent to the circle at point P on the circle without using the center of the circle
Do the following activity to draw tangents to the circle without using the center of the circle.
- Draw a circle with radius 3.5 cm and take any point C on it.
- Draw chord CB and an inscribed angle CAB.
- With the center A and any convenient radius, draw an arc intersecting the sides of angle BAC in points M and N.
- Using the same radius, draw an arc intersecting the chord CB at point R.
- Taking the radius equal to d(MN) and center R, draw an arc intersecting the arc drawn in the previous step. Let D be the point of intersection of these arcs. Draw line CD. Line CD is the required tangent to the circle.
Draw a circle with center O and radius 3.4. Draw a chord MN of length 5.7 cm in a circle. Draw tangents to the circle from point M and N
Draw a circle with center C and radius 3.2 cm. Draw a tangent to the circle from point P at a distance of 7.5 cm from the center of the circle
Draw a circle of radius 3 cm and draw chord XY 5 cm long. Draw the tangent of the circle passing through point X and point Y (without using the center of the circle)
Draw a circle with center O and radius 3 cm. Take the point P and the point Q at a distance of 7 cm from the center of the circle on the opposite side of the circle such that their line of intersection passing through the center of the circle Draw a tangent to the circle from the point P and the point Q
Draw any circle with radius greater than 1.8 cm and less than 3 cm. Draw a chord AB 3.6 cm long in this circle. Tangent to the circle passing through A and B without using the center of the circle
Draw a circle with center O and radius 2.8 cm. Take point P in the exterior of a circle such that tangents PA and PB drawn from point P make an angle ∠APB of measure 70°
