Advertisements
Advertisements
प्रश्न
Draw the ray diagram showing refraction of light through a glass prism and hence obtain the relation between the refractive index μ of the prism, angle of prism and angle of minimum deviation.
उत्तर
The figure below shows the passage of light through a triangular prism ABC.
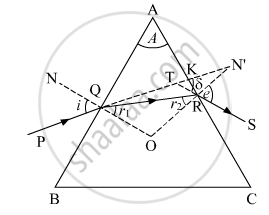
The angles of incidence and refraction at first face AB are ∠i and ∠r1.
The angle of incidence at the second face AC is ∠r2 and the angle of emergence ∠e.
δ is the angle between the emergent ray RS and incident ray PQ and is called the angle of deviation.
Here, ∠PQN = i
∠SRN'=e
∠RQO = r1
∠QRO = r2
∠KTS = δ
∴ ∠TQO = i and ∠RQO = r1, we have
∠TQR = i − r1
∠TRO = e and ∠QRO = r2
∠TRQ = e − r2
In triangle TQR, the side QT has been produced outwards. Therefore, the exterior angle δ should be equal to the sum of the interior opposite angles.
i.e, δ= ∠TQR + ∠TRQ = (i − r1) + (e − r2)
δ = (i + e) − (r1+ r2) ..…(i)
In triangle QRO,
r1+ r2+ ∠ROQ = 180° ..…(ii)
From quadrilateral AROQ, we have the sum of angles (∠AQO + ∠ARO = 180°). This means that the sum of the remaining two angles should be 180°.
i.e , ∠A + ∠QOR = 180° [∠A is called the angle of prism]
From equations (i) and (ii),
r1+ r2 = A (iii)
Substituting (iii) in (i), we obtain
δ = (i + e) − A
\[A + \delta = i + e\]
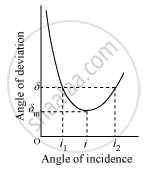
If the angle of incidence is increased gradually, then the angle of deviation first decreases, attains a minimum value (δm), and then again starts increasing.
When angle of deviation is minimum, the prism is said to be placed in the minimum deviation position.
There is only one angle of incidence for which the angle of deviation is minimum.
When
δ = δm [prism in minimum deviation position],
e = i and r2 = r1 = r …(iv)
\[\because r_1 + r_2 = A\]
From equation (iv), r + r = A
\[r = \frac{A}{2}\]
Also, we have
A + δ = i + e
Setting,
δ = δm and e = i
A + δm = i + i
\[i = \frac{\left( A + \delta_m \right)}{2}\]
\[ \because \mu = \frac{\sin i}{\sin r}\]
\[ \therefore \mu = \frac{\sin\left( \frac{A + \delta_m}{2} \right)}{\sin\left( \frac{A}{2} \right)}\]
APPEARS IN
संबंधित प्रश्न
Plot a graph to show the variation of the angle of deviation as a function of the angle of incidence for light passing through a prism. Derive an expression for the refractive index of the prism in terms of angle of minimum deviation and angle of the prism.
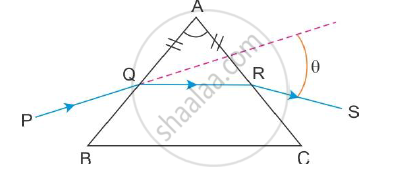
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60° and refractive index of material of prism is `sqrt3 `. Calculate angle θ.
Out of blue and red light which is deviated more by a prism? Give reason.
The equation \[\omega = \frac{\mu_u - \mu_r}{\mu - 1}\] was derived for a prism having small refracting angle. Is it also valid for a prism of large refracting angle? Is it also valid for a glass slab or a glass sphere?
Can the dispersive power \[\omega = \frac{\mu_u - \mu_r}{\mu - 1}\] be negative? What is the sign of ω if a hollow prism is immersed into water?
If a glass prism is dipped in water, its dispersive power ___________ .
A thin prism is made of a material having refractive indices 1.61 and 1.65 for red and violet light. The dispersive power of the material is 0.07. It is found that a beam of yellow light passing through the prism suffers a minimum deviation of 4.0° in favourable conditions. Calculate the angle of the prism.
The minimum deviations suffered by, yellow and violet beams passing through an equilateral transparent prism are 38.4°, 38.7° and 39.2° respectively. Calculate the dispersive power of the medium.
A thin prism of angle 6.0°, ω = 0.07 and μy = 1.50 is combined with another thin prism having ω = 0.08 and μy = 1.60. The combination produces no deviation in the mean ray. (a) Find the angle of the second prism. (b) Find the net angular dispersion produced by the combination when a beam of white light passes through it. (c) If the prisms are similarly directed, what will be the deviation in the mean ray? (d) Find the angular dispersion in the situation described in (c).
Define angular dispersion.
