Advertisements
Advertisements
प्रश्न
Drive the expression for electric field at a point on the equatorial line of an electric dipole.
उत्तर
Electric Field for Points on the Equatorial Plane:
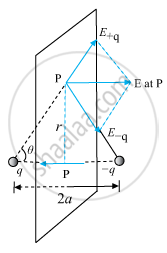
The magnitudes of the electric field due to the two charges +q and −q are given by,
`E_(+q)=q/(4piepsilon_0)1/(r^2+a^2)` .....(i)
`E_(-q)=q/(4piepsilon_0)1/(r^2-a^2)` .....(ii)
The directions of E+q and E−q are as shown in the figure. The components normal to the dipole axis cancel away. The components along the dipole axis add up.
∴ Total electric field
`E=-(E_(+q)+E_(-q))cos theta.hatp`[Negative sign shows that field is opposite to `hatp`]
`E=-(2qa)/(4piepsilon_0(r^2+a^2)^(3/2))hatp` .....(iii)
At large distances (r >> a), this reduces to
`E=-(2qa)/(4piepsilon_0(r^3))hatp` .....(iv)
`because vecp=qxxvec(2a)hatp`
`therefore E=(-vecp)/(4piepsilon_0(r^3))` (r >> a)
APPEARS IN
संबंधित प्रश्न
A short electric dipole (which consists of two point charges, +q and -q) is placed at the centre 0 and inside a large cube (ABCDEFGH) of length L, as shown in Figure 1. The electric flux, emanating through the cube is:
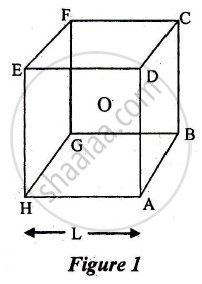
a) `q"/"4piin_9L`
b) zero
c) `q"/"2piin_0L`
d) `q"/"3piin_0L`
Derive an expression for the intensity of electric field at a point in broadside position or on [4)
an equatorial line of an electric dipole.
An electric dipole of length 1 cm, which placed with its axis making an angle of 60° with uniform electric field, experience a torque of \[6\sqrt{3} Nm\] . Calculate the potential energy of the dipole if it has charge ±2 nC.
Three charges are arranged on the vertices of an equilateral triangle, as shown in the figure. Find the dipole moment of the combination.
Two-point charges Q1 = 400 μC and Q2 = 100 μC are kept fixed, 60 cm apart in a vacuum. Find the intensity of the electric field at the midpoint of the line joining Q1 and Q2.
The electric intensity due to a dipole of length 10 cm and having a charge of 500 µC, at a point on the axis at a distance 20 cm from one of the charges in air, is:
The region surrounding a stationary electric dipole has ______
The electric potential V as a function of distance X is shown in the figure.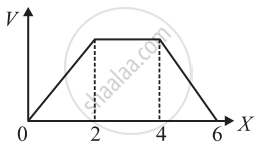
The graph of the magnitude of electric field intensity E as a function of X is ______.
Eight dipoles of charges of magnitude e each are placed inside a cube. The total electric flux coming out of the cube will be ______.
Show that intensity of electric field at a point in broadside position of an electric dipole is given by:
E = `(1/(4piepsilon_0)) "p"/(("r"^2 + l^2)^(3//2))`
Where the terms have their usual meaning.
