Advertisements
Advertisements
प्रश्न
एक अवतल पंचभुज है।
पर्याय
सत्य
असत्य
उत्तर
यह कथन असत्य है।
स्पष्टीकरण -
चूँकि इसकी 6 भुजाएँ हैं, इसलिए यह एक अवतल षट्भुज है।
APPEARS IN
संबंधित प्रश्न
तालिका की जांच कीजिए : (प्रत्येक आकृति को त्रिभुजों में बाँटिए और कोणों का योगफल ज्ञात कीजिए।)
| आकृति |  |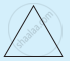
 |
 |
 |
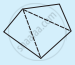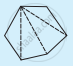| भुजा | 3 | 4 | 5 | 6 |
| कोणों का योगफल | 180° | 2 × 180° = (4 - 2) × 180° | 3 × 180° = (5 - 2) × 180° | 4 × 180° = (6 - 2) × 180° |
एक बहुभुज के कोणों के योग के बारे में आप क्या कह सकते हैं, जिसकी भुजाओं की संख्या निम्नलिखित हो।
- 7
- 8
- 10
- n
एक सम बहुभुज कितनी भुजाएँ होंगी यदि एक बाह्य कोण का माप 24° हो ?
एक सम बहुभुज की भुजाएँ की संख्या ज्ञात कीजिए यदि इसका प्रत्येक अंतः कोण 165° का हो?
क्या यह किसी सम बहुभुज का अंत:कोण हो सकता है? क्यों?
निम्न में से कौन एक समानकोणिक और समबाहु बहुभुज है?
प्रत्येक अंतःकोण 135∘ वाले एक समबहुभुज की भुजाओं की संख्या है –
एक सम पंचभुज के प्रत्येक कोण की माप ______ हैं।
एक सम बहुभुज वह बहुभुज है जिसकी सभी भुजाएँ बराबर होती हैं, और सभी ______ बराबर होते हैं।
10 भुजाओं वाला बहुभुज ______ कहलाता है।
यदि किसी बहुभुज के अंतःकोणों का योग उसके एक ही क्रम में लिए गए बहिष्कोणों के योग का दोगुना हो, तो वह एक षड्भुज होगा।
