Advertisements
Advertisements
प्रश्न
एक चतुर्भुज ABCD एक वृत्त के अंतर्गत इस प्रकार है कि AB वृत्त का व्यास है और ∠ADC = 130° है। ∠BAC ज्ञात कीजिए।
उत्तर
O केंद्र वाले एक वृत्त के अंतर्गत एक चतुर्भुज ABCD खींचिए।
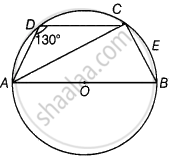
दिया गया है, ∠ADC = 130°
चूँकि, ABCD एक वृत्त में खुदा हुआ चतुर्भुज है, इसलिए ABCD एक चक्रीय चतुर्भुज बन जाता है।
∵ चूँकि, चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है।
∴ ∠ADC + ∠ABC = 180°
⇒ 130° + ∠ABC = 180°
⇒∠ABC = 50°
चूँकि, AB एक वृत्त का व्यास है, तो AB वृत्त के समकोण पर एक कोण अंतरित करता है।
∴ ∠ACB = 90°
∠ABC में, ∠BAC + ∠ACB + ∠ABC = 180° ...[त्रिभुज के कोण योग गुण द्वारा]
⇒ ∠BAC + 90° + 50° = 180°
⇒ ∠BAC = 180° – (90° + 50°)
= 180° – 140°
= 40°
APPEARS IN
संबंधित प्रश्न
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए।
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं । B से जाने वाले दो रेखाखंड ABD और PBQ वृतों को A, D और P, Q पर क्रमश: प्रतिछेद करते हुए खींचे गए हैं (देखिए आकृति में)। सिद्ध कीजिए कि ∠ACP = ∠QCD है।

सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों के केंद्रों की रेखा प्रतिच्छेदन के दो बिंदुओं पर समान कोण अंतरित करती है।
एक त्रिभुज ABC के कोण A, B और C के समद्विभाजक इसके परिवृत्त को क्रमशः D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि त्रिभुज DEF के कोण हैं `90^@-1/2A, 90^@-1/2B" तथा "90^@-1/2C` हैं
ABCD एक चक्रीय चतुर्भुज है, जिसमें ∠A = 90°, ∠B = 70°, ∠C = 95° और ∠D = 105° है।
यदि A, B, C और D चार बिंदु इस प्रकार हैं कि ∠BAC = 45° और ∠BDC = 45° है, तो A, B, C और D चक्रीय है।
ABCD एक ऐसा चतुर्भुज है कि A शीर्षों B, C और D से होकर जाने वाले वृत्त का केंद्र है। सिद्ध कीजिए कि ∠CBD + ∠CDB = `1/2` ∠BAD है।
यदि किसी समद्विबाहु त्रिभुज के आधार के समांतर कोई रेखा उसकी बराबर भुजाओं को प्रतिच्छेद करने के लिए खींची जाए, तो सिद्ध कीजिए कि इस प्रकार बना चतुर्भुज चक्रीय होता है।
