Advertisements
Advertisements
प्रश्न
ABCD एक ऐसा चतुर्भुज है कि A शीर्षों B, C और D से होकर जाने वाले वृत्त का केंद्र है। सिद्ध कीजिए कि ∠CBD + ∠CDB = `1/2` ∠BAD है।
उत्तर
एक वृत्त में, ABCD एक चतुर्भुज है जिसका केंद्र A है।
सिद्ध करना है ∠CBD + ∠CDB = `1/2` ∠BAD
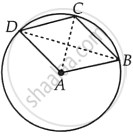
रचना - AC को मिलाइए।
उपपत्ति - जैसा कि हम जानते हैं कि किसी चाप द्वारा केंद्र पर बनाया गया कोण वृत्त के शेष भाग पर बने बिंदु पर बनाए गए कोण का दुगुना होता है।
इसलिए, ∠CAD = 2∠CBD ...(i)
और ∠BAC = 2∠CDB ...(ii)
अब, समीकरण (i) और (ii) को जोड़ने पर, हम प्राप्त करते हैं।
∠CAD + ∠BAC = 2(∠CBD + ∠CDB)
∠BAD = 2(∠CBD + ∠CDB)
अत:, ∠CBD + ∠CDB = `1/2` ∠BAD।
APPEARS IN
संबंधित प्रश्न
ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात कीजिए। पुनः यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए।
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
सिद्ध कीजिए कि एक चक्रीय समांतर चतुर्भुज एक आयत होता है।
एक वृत्त की दो समानांतर जीवाओं की लंबाई 6 सेमी और 8 सेमी है। यदि छोटी जीवा केंद्र से 4 सेमी की दूरी पर है, तो केंद्र से दूसरी जीवा की दूरी क्या है?
ABCD एक समांतर चतुर्भुज है। A, B और C से होकर जाने वाला वृत्त, CD (यदि आवश्यक हो तो) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।
दो सर्वांगसम वृत्त परस्पर बिंदुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लंब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
ABCD एक चक्रीय चतुर्भुज है, जिसमें ∠A = 90°, ∠B = 70°, ∠C = 95° और ∠D = 105° है।
यदि A, B, C और D चार बिंदु इस प्रकार हैं कि ∠BAC = 45° और ∠BDC = 45° है, तो A, B, C और D चक्रीय है।
एक चतुर्भुज ABCD एक वृत्त के अंतर्गत इस प्रकार है कि AB वृत्त का व्यास है और ∠ADC = 130° है। ∠BAC ज्ञात कीजिए।
