Advertisements
Advertisements
प्रश्न
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लंब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
Advertisements
उत्तर
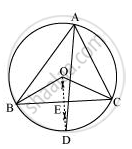
माना भुजा BC का लंब समद्विभाजक और ∠A का कोण समद्विभाजक बिंदु D पर मिलता है। मान लीजिए कि भुजा BC का लंब समद्विभाजक इसे E पर प्रतिच्छेद करता है।
भुजा BC का लंब समद्विभाजक वृत्त के परिकेन्द्र O से होकर जाएगा। ∠BOC और ∠BAC चाप BC द्वारा वृत्त के शेष भाग पर क्रमशः केंद्र पर और एक बिंदु A द्वारा अंतरित कोण हैं। हम यह भी जानते हैं कि एक चाप द्वारा केंद्र पर बनाया गया कोण वृत्त के शेष भाग पर किसी भी बिंदु पर इसके द्वारा बनाए गए कोण का दोगुना होता है।
∠BOC = 2 ∠BAC = 2 ∠A ... (1)
In ΔBOE तथा ΔCOE,
OE = OE (सामान्य)
OB = OC (एक ही वृत्त की त्रिज्या)
∠OEB = ∠OEC (प्रत्येक 90° as OD ⊥ BC)
∴ ΔBOE ≅ ∠COE (RHS सर्वांगसमता नियम)
∠BOE = ∠COE (By CPCT) ... (2)
हालाँकि, ∠BOE + ∠COE = ∠BOC
⇒ ∠BOE +∠BOE = 2 ∠A [समीकरण (1) और (2) का उपयोग करना]
⇒ 2 ∠BOE = 2 ∠A
⇒ ∠BOE = ∠A
∴ ∠BOE = ∠COE = ∠A
भुजा BC का लंब समद्विभाजक और ∠A का कोण समद्विभाजक बिंदु ∠D पर मिलते हैं।
∴ ∠BOD = ∠BOE = ∠A ... (3)
चूँकि AD कोण का समद्विभाजक है ∠A,
∠BAD = ∠A/2
⇒ 2 ∠BAD = ∠A ... (4)
समीकरण (3) और (4) से, हम प्राप्त करते हैं
∠BOD = 2 ∠BAD
यह तभी संभव हो सकता है जब बिंदु BD वृत्त की जीवा हो। इसके लिए बिंदु D वृत्त वृत्त पर स्थित है।
अत: भुजा BC का लम्ब समद्विभाजक और ∠A का कोण समद्विभाजक त्रिभुज ABC के परिवृत्त पर मिलते हैं।
संबंधित प्रश्न
आकृति में, ∠PQR = 100° है, जहाँ P, Q तथा R केंद्र O वाले एक वृत्त पर स्थित बिंदु हैं। ∠OPR ज्ञात कीजिए।
ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात कीजिए। पुनः यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए।
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं । B से जाने वाले दो रेखाखंड ABD और PBQ वृतों को A, D और P, Q पर क्रमश: प्रतिछेद करते हुए खींचे गए हैं (देखिए आकृति में)। सिद्ध कीजिए कि ∠ACP = ∠QCD है।
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
एक वृत्त की दो समानांतर जीवाओं की लंबाई 6 सेमी और 8 सेमी है। यदि छोटी जीवा केंद्र से 4 सेमी की दूरी पर है, तो केंद्र से दूसरी जीवा की दूरी क्या है?
ABCD एक समांतर चतुर्भुज है। A, B और C से होकर जाने वाला वृत्त, CD (यदि आवश्यक हो तो) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।
दो सर्वांगसम वृत्त परस्पर बिंदुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।
ABCD एक ऐसा चतुर्भुज है कि A शीर्षों B, C और D से होकर जाने वाले वृत्त का केंद्र है। सिद्ध कीजिए कि ∠CBD + ∠CDB = `1/2` ∠BAD है।
एक चतुर्भुज ABCD एक वृत्त के अंतर्गत इस प्रकार है कि AB वृत्त का व्यास है और ∠ADC = 130° है। ∠BAC ज्ञात कीजिए।
