Advertisements
Advertisements
Question
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लंब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
Solution
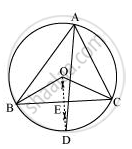
माना भुजा BC का लंब समद्विभाजक और ∠A का कोण समद्विभाजक बिंदु D पर मिलता है। मान लीजिए कि भुजा BC का लंब समद्विभाजक इसे E पर प्रतिच्छेद करता है।
भुजा BC का लंब समद्विभाजक वृत्त के परिकेन्द्र O से होकर जाएगा। ∠BOC और ∠BAC चाप BC द्वारा वृत्त के शेष भाग पर क्रमशः केंद्र पर और एक बिंदु A द्वारा अंतरित कोण हैं। हम यह भी जानते हैं कि एक चाप द्वारा केंद्र पर बनाया गया कोण वृत्त के शेष भाग पर किसी भी बिंदु पर इसके द्वारा बनाए गए कोण का दोगुना होता है।
∠BOC = 2 ∠BAC = 2 ∠A ... (1)
In ΔBOE तथा ΔCOE,
OE = OE (सामान्य)
OB = OC (एक ही वृत्त की त्रिज्या)
∠OEB = ∠OEC (प्रत्येक 90° as OD ⊥ BC)
∴ ΔBOE ≅ ∠COE (RHS सर्वांगसमता नियम)
∠BOE = ∠COE (By CPCT) ... (2)
हालाँकि, ∠BOE + ∠COE = ∠BOC
⇒ ∠BOE +∠BOE = 2 ∠A [समीकरण (1) और (2) का उपयोग करना]
⇒ 2 ∠BOE = 2 ∠A
⇒ ∠BOE = ∠A
∴ ∠BOE = ∠COE = ∠A
भुजा BC का लंब समद्विभाजक और ∠A का कोण समद्विभाजक बिंदु ∠D पर मिलते हैं।
∴ ∠BOD = ∠BOE = ∠A ... (3)
चूँकि AD कोण का समद्विभाजक है ∠A,
∠BAD = ∠A/2
⇒ 2 ∠BAD = ∠A ... (4)
समीकरण (3) और (4) से, हम प्राप्त करते हैं
∠BOD = 2 ∠BAD
यह तभी संभव हो सकता है जब बिंदु BD वृत्त की जीवा हो। इसके लिए बिंदु D वृत्त वृत्त पर स्थित है।
अत: भुजा BC का लम्ब समद्विभाजक और ∠A का कोण समद्विभाजक त्रिभुज ABC के परिवृत्त पर मिलते हैं।
APPEARS IN
RELATED QUESTIONS
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए।
आकृति में, ∠PQR = 100° है, जहाँ P, Q तथा R केंद्र O वाले एक वृत्त पर स्थित बिंदु हैं। ∠OPR ज्ञात कीजिए।

सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों के केंद्रों की रेखा प्रतिच्छेदन के दो बिंदुओं पर समान कोण अंतरित करती है।
मान लीजिए कि एक कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त के साथ समान जीवाओं AD और CE को प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∠ABC, जीवाओं AC और DE द्वारा केंद्र में अंतरित कोणों के अंतर के आधे के बराबर है।
सिद्ध कीजिए कि किसी समचतुर्भुज की किसी भुजा को व्यास मानकर खींचा गया वृत्त उसके विकर्णों के प्रतिच्छेदन बिंदु से होकर गुजरता है।
AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित होती हैं। सिद्ध कीजिए:
(I) AC और BD व्यास हैं,
(Ii) ABCD एक आयत है।
यदि किसी समद्विबाहु त्रिभुज के आधार के समांतर कोई रेखा उसकी बराबर भुजाओं को प्रतिच्छेद करने के लिए खींची जाए, तो सिद्ध कीजिए कि इस प्रकार बना चतुर्भुज चक्रीय होता है।
यदि किसी चक्रीय चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर है, तो सिद्ध कीजिए कि इसके विकर्ण भी बराबर हैं।
एक चतुर्भुज ABCD एक वृत्त के अंतर्गत इस प्रकार है कि AB वृत्त का व्यास है और ∠ADC = 130° है। ∠BAC ज्ञात कीजिए।
यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि यह एक चक्रीय है।
