Advertisements
Advertisements
Question
यदि किसी समद्विबाहु त्रिभुज के आधार के समांतर कोई रेखा उसकी बराबर भुजाओं को प्रतिच्छेद करने के लिए खींची जाए, तो सिद्ध कीजिए कि इस प्रकार बना चतुर्भुज चक्रीय होता है।
Solution
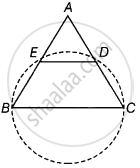
दिया गया है - ΔABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC और DE || BC है।
सिद्ध करना है - चतुर्भुज BCDE एक चक्रीय चतुर्भुज है।
रचना - बिंदुओं B, C, D और E से होकर जाने वाला एक वृत्त खींचिए।
प्रमाण - ΔABC में, AB = AC ...[एक समद्विबाहु त्रिभुज की समान भुजाएँ]
⇒ ∠ACB = ∠ABC ...(i)
चूंकि, DE || BC ...[समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
⇒ ∠ADE = ∠ACB [संगत कोण] ...(ii)
समीकरण (ii) में दोनों पक्षों को ∠EDC से जोड़ने पर, हम पाते हैं।
∠ADE + ∠EDC = ∠ACB + ∠EDC
⇒ 180° = ∠ACB + ∠EDC ...[∠ADE और ∠EDC रैखिक युग्म एनिओम से]
⇒ ∠EDC + ∠ABC = 180° ...[समीकरण (i) से]
अत:, BCDE एक चक्रीय चतुर्भुज है, क्योंकि सम्मुख कोणों का योग 180° होता है।
APPEARS IN
RELATED QUESTIONS
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
सिद्ध कीजिए कि एक चक्रीय समांतर चतुर्भुज एक आयत होता है।
सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों के केंद्रों की रेखा प्रतिच्छेदन के दो बिंदुओं पर समान कोण अंतरित करती है।
मान लीजिए कि एक कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त के साथ समान जीवाओं AD और CE को प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∠ABC, जीवाओं AC और DE द्वारा केंद्र में अंतरित कोणों के अंतर के आधे के बराबर है।
एक त्रिभुज ABC के कोण A, B और C के समद्विभाजक इसके परिवृत्त को क्रमशः D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि त्रिभुज DEF के कोण हैं `90^@-1/2A, 90^@-1/2B" तथा "90^@-1/2C` हैं
दो सर्वांगसम वृत्त परस्पर बिंदुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लंब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
यदि A, B, C और D चार बिंदु इस प्रकार हैं कि ∠BAC = 45° और ∠BDC = 45° है, तो A, B, C और D चक्रीय है।
यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि यह एक चक्रीय है।
