Advertisements
Advertisements
Question
AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित होती हैं। सिद्ध कीजिए:
(I) AC और BD व्यास हैं,
(Ii) ABCD एक आयत है।
Solution
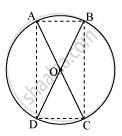
मान लीजिए कि दो जीवाएँ AB और CD एक दूसरे को बिंदु O पर काट रही हैं।
In ΔAOB तथा ΔCOD,
OA = OC (दिया गया)
OB = OD (दिया गया)
∠AOB = ∠COD (लंबवत विपरीत कोण)
ΔAOB ≅ ΔCOD (SAS सर्वांगसमता नियम)
AB = CD (By CPCT)
इसी प्रकार, यह सिद्ध किया जा सकता है कि ΔAOD ≅ ΔCOB
∴ AD = CB (By CPCT)
चूँकि चतुर्भुज ACBD में, सम्मुख भुजाएँ लंबाई में बराबर होती हैं, ACBD एक समांतर चतुर्भुज है।
हम जानते हैं कि समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
∴ ∠A = ∠C
हालाँकि, A + C = 180° (ABCD एक चक्रीय चतुर्भुज है)
⇒ ∠A + ∠A = 180°
⇒ 2 ∠A = 180°
⇒ ∠A = 90°
चूँकि ACBD एक समांतर चतुर्भुज है और इसका एक आंतरिक कोण 90° का है, इसलिए यह एक आयत है।
∠A जीवा BD द्वारा अंतरित कोण है। और चूँकि ∠A = 90° है, इसलिए BD वृत्त का व्यास होना चाहिए। इसी प्रकार, AC वृत्त का व्यास है।
APPEARS IN
RELATED QUESTIONS
ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात कीजिए। पुनः यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए।
दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं । B से जाने वाले दो रेखाखंड ABD और PBQ वृतों को A, D और P, Q पर क्रमश: प्रतिछेद करते हुए खींचे गए हैं (देखिए आकृति में)। सिद्ध कीजिए कि ∠ACP = ∠QCD है।

यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
सिद्ध कीजिए कि एक चक्रीय समांतर चतुर्भुज एक आयत होता है।
एक वृत्त की क्रमशः 5 सेमी 11 सेमी लम्बाई की दो जीवाएँ AB और CD एक दूसरे के समानांतर हैं और इसके केंद्र के विपरीत दिशा में हैं। यदि AB और CD के बीच की दूरी 6 सेमी है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
मान लीजिए कि एक कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त के साथ समान जीवाओं AD और CE को प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∠ABC, जीवाओं AC और DE द्वारा केंद्र में अंतरित कोणों के अंतर के आधे के बराबर है।
ABCD एक समांतर चतुर्भुज है। A, B और C से होकर जाने वाला वृत्त, CD (यदि आवश्यक हो तो) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।
यदि किसी समद्विबाहु त्रिभुज के आधार के समांतर कोई रेखा उसकी बराबर भुजाओं को प्रतिच्छेद करने के लिए खींची जाए, तो सिद्ध कीजिए कि इस प्रकार बना चतुर्भुज चक्रीय होता है।
यदि किसी चक्रीय चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर है, तो सिद्ध कीजिए कि इसके विकर्ण भी बराबर हैं।
एक चतुर्भुज ABCD एक वृत्त के अंतर्गत इस प्रकार है कि AB वृत्त का व्यास है और ∠ADC = 130° है। ∠BAC ज्ञात कीजिए।
