Advertisements
Advertisements
Question
एक वृत्त की क्रमशः 5 सेमी 11 सेमी लम्बाई की दो जीवाएँ AB और CD एक दूसरे के समानांतर हैं और इसके केंद्र के विपरीत दिशा में हैं। यदि AB और CD के बीच की दूरी 6 सेमी है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
Solution
OM ⊥ AB और ON ⊥ CD बनाइए। OB और OD को मिलाइए।
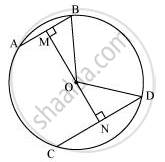
BM = AB/2 = 5/2 (केंद्र से लंबवत जीवा को समद्विभाजित करता है)
ND = CD/2 = 11/2
चलो ON हो x इसलिए, OM 6− x होगा।
In ΔMOB,
OM2 + MB2 = OB2
(6 - x)2 + (5/2)2 = OB2
36 + x2 - 12x + 25/4 = OB2 ........(1)
In ΔNOD,
ON2 + ND2 = OD2
x2 + (11/2)2 = OD2
x2 + 121/4 = OD2 .........(2)
हमारे पास OB = OD (उसी वृत्त की त्रिज्याएँ) हैं।
इसलिए, समीकरण (1) और (2) से,
`36+x^2-12x+25/4=x^2+121/4`
`12x=36+24/4-121/4`
`=(144+25-121)/4`
`=48/4`
= 12
x = 1
समीकरण (2) से,
`(1)^2+(121/4)=OD^2`
`OD^2 = 1+121/4=125/4`
`OD=5/2sqrt5`
इसलिए, वृत्त की त्रिज्या है `5/2sqrt5" cm."`
APPEARS IN
RELATED QUESTIONS
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠CAD = ∠CBD हैं।
मान लीजिए कि एक कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त के साथ समान जीवाओं AD और CE को प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∠ABC, जीवाओं AC और DE द्वारा केंद्र में अंतरित कोणों के अंतर के आधे के बराबर है।
ABCD एक समांतर चतुर्भुज है। A, B और C से होकर जाने वाला वृत्त, CD (यदि आवश्यक हो तो) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।
एक त्रिभुज ABC के कोण A, B और C के समद्विभाजक इसके परिवृत्त को क्रमशः D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि त्रिभुज DEF के कोण हैं `90^@-1/2A, 90^@-1/2B" तथा "90^@-1/2C` हैं
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लंब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
यदि A, B, C और D चार बिंदु इस प्रकार हैं कि ∠BAC = 45° और ∠BDC = 45° है, तो A, B, C और D चक्रीय है।
यदि किसी चक्रीय चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर है, तो सिद्ध कीजिए कि इसके विकर्ण भी बराबर हैं।
