Advertisements
Advertisements
प्रश्न
एक वृत्त की क्रमशः 5 सेमी 11 सेमी लम्बाई की दो जीवाएँ AB और CD एक दूसरे के समानांतर हैं और इसके केंद्र के विपरीत दिशा में हैं। यदि AB और CD के बीच की दूरी 6 सेमी है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
उत्तर
OM ⊥ AB और ON ⊥ CD बनाइए। OB और OD को मिलाइए।
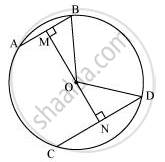
BM = AB/2 = 5/2 (केंद्र से लंबवत जीवा को समद्विभाजित करता है)
ND = CD/2 = 11/2
चलो ON हो x इसलिए, OM 6− x होगा।
In ΔMOB,
OM2 + MB2 = OB2
(6 - x)2 + (5/2)2 = OB2
36 + x2 - 12x + 25/4 = OB2 ........(1)
In ΔNOD,
ON2 + ND2 = OD2
x2 + (11/2)2 = OD2
x2 + 121/4 = OD2 .........(2)
हमारे पास OB = OD (उसी वृत्त की त्रिज्याएँ) हैं।
इसलिए, समीकरण (1) और (2) से,
`36+x^2-12x+25/4=x^2+121/4`
`12x=36+24/4-121/4`
`=(144+25-121)/4`
`=48/4`
= 12
x = 1
समीकरण (2) से,
`(1)^2+(121/4)=OD^2`
`OD^2 = 1+121/4=125/4`
`OD=5/2sqrt5`
इसलिए, वृत्त की त्रिज्या है `5/2sqrt5" cm."`
APPEARS IN
संबंधित प्रश्न
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए।
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
सिद्ध कीजिए कि एक चक्रीय समांतर चतुर्भुज एक आयत होता है।
सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों के केंद्रों की रेखा प्रतिच्छेदन के दो बिंदुओं पर समान कोण अंतरित करती है।
एक त्रिभुज ABC के कोण A, B और C के समद्विभाजक इसके परिवृत्त को क्रमशः D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि त्रिभुज DEF के कोण हैं `90^@-1/2A, 90^@-1/2B" तथा "90^@-1/2C` हैं
दो सर्वांगसम वृत्त परस्पर बिंदुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।
यदि A, B, C और D चार बिंदु इस प्रकार हैं कि ∠BAC = 45° और ∠BDC = 45° है, तो A, B, C और D चक्रीय है।
यदि किसी समद्विबाहु त्रिभुज के आधार के समांतर कोई रेखा उसकी बराबर भुजाओं को प्रतिच्छेद करने के लिए खींची जाए, तो सिद्ध कीजिए कि इस प्रकार बना चतुर्भुज चक्रीय होता है।
यदि किसी चक्रीय चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर है, तो सिद्ध कीजिए कि इसके विकर्ण भी बराबर हैं।
एक चतुर्भुज ABCD एक वृत्त के अंतर्गत इस प्रकार है कि AB वृत्त का व्यास है और ∠ADC = 130° है। ∠BAC ज्ञात कीजिए।
