Advertisements
Advertisements
प्रश्न
यदि किसी चक्रीय चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर है, तो सिद्ध कीजिए कि इसके विकर्ण भी बराबर हैं।
उत्तर
दिया गया है - मान लीजिए ABCD एक चक्रीय चतुर्भुज है और AD = BC है।
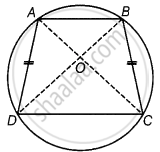
AC और BD को मिलाइए।
सिद्ध करना है - AC = BD
प्रमाण - ΔAOD और ΔBOC में,
∠OAD = ∠OBC और ∠ODA = ∠OCB ...[चूंकि समान खंड वृत्त पर समान कोण अंतरित करते हैं।]
AB = BC ...[दिया गया है।]
ΔAOD = ΔBOC ...[ASA सर्वांगसमता नियम द्वारा]
जोड़ने पर दोनों ओर DOC होता है, हम पाते हैं।
ΔAOD + ΔDOC ≅ ΔBOC + ΔDOC
⇒ ΔADC ≅ ΔBCD
AC = BD ...[CPCT द्वारा]
APPEARS IN
संबंधित प्रश्न
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए।
आकृति में, ∠PQR = 100° है, जहाँ P, Q तथा R केंद्र O वाले एक वृत्त पर स्थित बिंदु हैं। ∠OPR ज्ञात कीजिए।

दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं । B से जाने वाले दो रेखाखंड ABD और PBQ वृतों को A, D और P, Q पर क्रमश: प्रतिछेद करते हुए खींचे गए हैं (देखिए आकृति में)। सिद्ध कीजिए कि ∠ACP = ∠QCD है।

यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠CAD = ∠CBD हैं।
सिद्ध कीजिए कि एक चक्रीय समांतर चतुर्भुज एक आयत होता है।
ABCD एक समांतर चतुर्भुज है। A, B और C से होकर जाने वाला वृत्त, CD (यदि आवश्यक हो तो) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।
AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित होती हैं। सिद्ध कीजिए:
(I) AC और BD व्यास हैं,
(Ii) ABCD एक आयत है।
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लंब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
एक चतुर्भुज ABCD एक वृत्त के अंतर्गत इस प्रकार है कि AB वृत्त का व्यास है और ∠ADC = 130° है। ∠BAC ज्ञात कीजिए।
