Advertisements
Advertisements
प्रश्न
यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि यह एक चक्रीय है।
उत्तर
दिया गया है - ABCD एक समलंब है जिसकी असमांतर भुजाएँ AD और BC बराबर हैं।
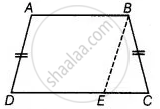
सिद्ध करना है - समलंब ABCD चक्रीय है।
BE को मिलाने पर, जहाँ BE || AD
प्रमाण - चूँकि, AB || DE और AD || BE
चूँकि, चतुर्भुज ABED एक समांतर चतुर्भुज है।
∴ ∠BAD = ∠BED ...(i) [समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।]
तथा AD = BE ...(ii) [समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।]
लेकिन AD = BC [दिया गया है।] ...(iii)
समीकरण (ii) और (iii) से,
BC = BE
⇒ ∠BEC = ∠BCE ...(iv) [समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
साथ ही, ∠BEC + ∠BED = 180° ...[रैखिक युग्म अभिगृहीत]
∴ ∠BCE + ∠BAD = 180° ...[समीकरण (i) और (iv) से]
यदि किसी चतुर्भुज के सम्मुख कोणों का योग 180° हो, तो चतुर्भुज चक्रीय होता है।
अत:, समलंब ABCD एक चक्रीय है।
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
आकृति में, ∠PQR = 100° है, जहाँ P, Q तथा R केंद्र O वाले एक वृत्त पर स्थित बिंदु हैं। ∠OPR ज्ञात कीजिए।

ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात कीजिए। पुनः यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए।
उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠CAD = ∠CBD हैं।
एक वृत्त की क्रमशः 5 सेमी 11 सेमी लम्बाई की दो जीवाएँ AB और CD एक दूसरे के समानांतर हैं और इसके केंद्र के विपरीत दिशा में हैं। यदि AB और CD के बीच की दूरी 6 सेमी है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
सिद्ध कीजिए कि किसी समचतुर्भुज की किसी भुजा को व्यास मानकर खींचा गया वृत्त उसके विकर्णों के प्रतिच्छेदन बिंदु से होकर गुजरता है।
ABCD एक चक्रीय चतुर्भुज है, जिसमें ∠A = 90°, ∠B = 70°, ∠C = 95° और ∠D = 105° है।
ABCD एक ऐसा चतुर्भुज है कि A शीर्षों B, C और D से होकर जाने वाले वृत्त का केंद्र है। सिद्ध कीजिए कि ∠CBD + ∠CDB = `1/2` ∠BAD है।
यदि किसी समद्विबाहु त्रिभुज के आधार के समांतर कोई रेखा उसकी बराबर भुजाओं को प्रतिच्छेद करने के लिए खींची जाए, तो सिद्ध कीजिए कि इस प्रकार बना चतुर्भुज चक्रीय होता है।
यदि किसी चक्रीय चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर है, तो सिद्ध कीजिए कि इसके विकर्ण भी बराबर हैं।
एक चतुर्भुज ABCD एक वृत्त के अंतर्गत इस प्रकार है कि AB वृत्त का व्यास है और ∠ADC = 130° है। ∠BAC ज्ञात कीजिए।
