Advertisements
Advertisements
Question
ABCD एक ऐसा चतुर्भुज है कि A शीर्षों B, C और D से होकर जाने वाले वृत्त का केंद्र है। सिद्ध कीजिए कि ∠CBD + ∠CDB = `1/2` ∠BAD है।
Solution
एक वृत्त में, ABCD एक चतुर्भुज है जिसका केंद्र A है।
सिद्ध करना है ∠CBD + ∠CDB = `1/2` ∠BAD
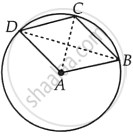
रचना - AC को मिलाइए।
उपपत्ति - जैसा कि हम जानते हैं कि किसी चाप द्वारा केंद्र पर बनाया गया कोण वृत्त के शेष भाग पर बने बिंदु पर बनाए गए कोण का दुगुना होता है।
इसलिए, ∠CAD = 2∠CBD ...(i)
और ∠BAC = 2∠CDB ...(ii)
अब, समीकरण (i) और (ii) को जोड़ने पर, हम प्राप्त करते हैं।
∠CAD + ∠BAC = 2(∠CBD + ∠CDB)
∠BAD = 2(∠CBD + ∠CDB)
अत:, ∠CBD + ∠CDB = `1/2` ∠BAD।
APPEARS IN
RELATED QUESTIONS
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए।
आकृति में, ∠PQR = 100° है, जहाँ P, Q तथा R केंद्र O वाले एक वृत्त पर स्थित बिंदु हैं। ∠OPR ज्ञात कीजिए।

यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
सिद्ध कीजिए कि एक चक्रीय समांतर चतुर्भुज एक आयत होता है।
सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों के केंद्रों की रेखा प्रतिच्छेदन के दो बिंदुओं पर समान कोण अंतरित करती है।
ABCD एक समांतर चतुर्भुज है। A, B और C से होकर जाने वाला वृत्त, CD (यदि आवश्यक हो तो) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।
एक त्रिभुज ABC के कोण A, B और C के समद्विभाजक इसके परिवृत्त को क्रमशः D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि त्रिभुज DEF के कोण हैं `90^@-1/2A, 90^@-1/2B" तथा "90^@-1/2C` हैं
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लंब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
यदि किसी समद्विबाहु त्रिभुज के आधार के समांतर कोई रेखा उसकी बराबर भुजाओं को प्रतिच्छेद करने के लिए खींची जाए, तो सिद्ध कीजिए कि इस प्रकार बना चतुर्भुज चक्रीय होता है।
