Advertisements
Advertisements
Question
O त्रिभुज ABC का परिकेंद्र है तथा D आधार BC का मध्य-बिंदु है। सिद्ध कीजिए कि ∠BOD = ∠A है।
Solution
दिया गया है - O त्रिभुज ABC का परिकेन्द्र है और D, BC का मध्य-बिंदु है।
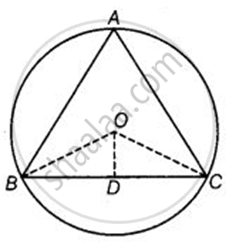
सिद्ध करना है - ∠BOD = ∠A
OB और OC को मिलाइए।
ΔOBD और ΔCD में,
OD = OD ...(उभयनिष्ठ पक्ष)
DB = Dc . ...(D, BC का मध्य-बिंदु है।)
OB = OC ...(दोनों वृत्त की त्रिज्या हैं।)
SSS सर्वांगसमता नियम से, ΔOBD ≅ ΔOCD।
∴ ∠BOD = ∠COD = x (माना) ...(CPCT द्वारा)
चूंकि, एक चाप द्वारा वृत्त के केंद्र पर बनाया गया कोण वृत्त के शेष भाग में किसी अन्य बिंदु पर बनाए गए कोण का दुगुना होता है, इसलिए हमारे पास है -
2∠BAC = ∠BOC
⇒ 2∠BAC = ∠BOD + ∠DOC
⇒ 2∠BAC = x + x
⇒ 2∠BAC = 2x
⇒ ∠BAC = x
⇒ ∠BAC = ∠BOD
अत: सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
एक वृत्त, जिस तल पर स्थित है, उसे _______ भागों में विभाजित करता है।
एक वृत्त में समान लंबाई की परिमित जीवाएँ होती हैं।
संलग्न आकृति देखकर लिखिए:
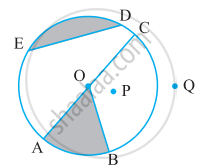
एक त्रिज्यखंड
निम्नलिखित आकृति में, यदि AOB वृत्त का एक व्यास तथा AC = BC है, तो ∠CAB बराबर है
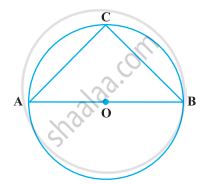
निम्नलिखित आकृति में, यदि ∠DAB = 60°, ∠ABD = 50° है, तो ∠ACB बराबर है
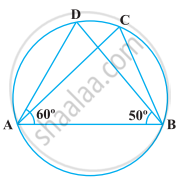
AOB वृत्त का एक व्यास है तथा C वृत्त पर स्थित कोई बिंदु है। तब, AC2 + BC2 = AB2 है।
एक वृत्त की दो जीवाएँ AB और AC उसके केंद्र पर क्रमश : 90° और 150° के कोण अंतरित करती हैं। ∠BAC ज्ञात कीजिए, यदि AB और AC केंद्र के विपरीत ओर स्थित हैं।
आकृति में O एक वृत्त का केंद्र है। त्रिज्याखंड OAC और OPB को छायांकित'कीजिए।
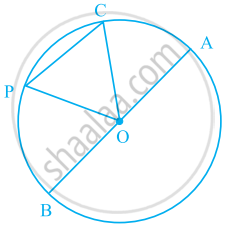
आकृति में O एक वृत्त का केंद्र है। CP द्वारा बनने वाले वृत्त के लघु वृत्तखंड को छायांकित कीजिए।
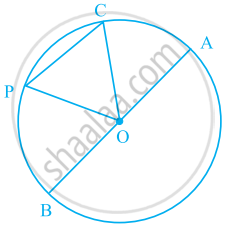
किसी वृत्त की समांतर जीवाओं की लंबाई क्रमशः 6 सेमी तथा 8 सेमी है। उस वृत्त की त्रिज्या 5 सेमी हो तो उन जीवाओं के बीच दूरी कितनी होगी?
