Advertisements
Advertisements
प्रश्न
O त्रिभुज ABC का परिकेंद्र है तथा D आधार BC का मध्य-बिंदु है। सिद्ध कीजिए कि ∠BOD = ∠A है।
उत्तर
दिया गया है - O त्रिभुज ABC का परिकेन्द्र है और D, BC का मध्य-बिंदु है।
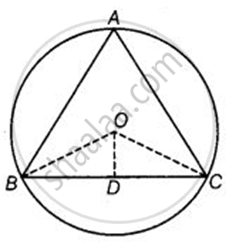
सिद्ध करना है - ∠BOD = ∠A
OB और OC को मिलाइए।
ΔOBD और ΔCD में,
OD = OD ...(उभयनिष्ठ पक्ष)
DB = Dc . ...(D, BC का मध्य-बिंदु है।)
OB = OC ...(दोनों वृत्त की त्रिज्या हैं।)
SSS सर्वांगसमता नियम से, ΔOBD ≅ ΔOCD।
∴ ∠BOD = ∠COD = x (माना) ...(CPCT द्वारा)
चूंकि, एक चाप द्वारा वृत्त के केंद्र पर बनाया गया कोण वृत्त के शेष भाग में किसी अन्य बिंदु पर बनाए गए कोण का दुगुना होता है, इसलिए हमारे पास है -
2∠BAC = ∠BOC
⇒ 2∠BAC = ∠BOD + ∠DOC
⇒ 2∠BAC = x + x
⇒ 2∠BAC = 2x
⇒ ∠BAC = x
⇒ ∠BAC = ∠BOD
अत: सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
वृत्त का केन्द्र वृत्त के ______ में स्थित है।
एक चाप _______ होता है, जब इसके सिरे एक व्यास के सिरे हों।
वृत्त एक समतल आकृति है।
किसी वृत्त का AD एक व्यास है और AB एक जीवा है। यदि AD = 34 cm, AB = 30 cm है, तो वृत्त के केंद्र से AB की दूरी है
निम्नलिखित आकृति में, यदि ∠ABC = 20° है, तो ∠AOC बराबर है
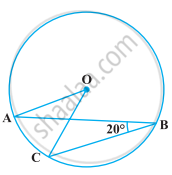
यदि एक वृत्त PXAQBY की एक जीवा AB का लंब समद्विभाजक वृत्त को P और Q बिंदुओं पर प्रतिच्छेद करता है, तो सिद्ध कीजिए कि चाप PXA ≅ चाप PYB हैं।
एक वृत्त की दो जीवाएँ AB और AC उसके केंद्र पर क्रमश : 90° और 150° के कोण अंतरित करती हैं। ∠BAC ज्ञात कीजिए, यदि AB और AC केंद्र के विपरीत ओर स्थित हैं।
आकृति में O एक वृत्त का केंद्र है। वृत्त की सभी त्रिज्याओं के नाम लिखिए।
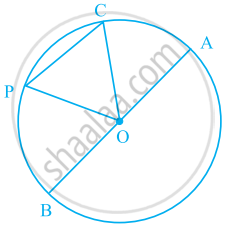
आकृति में O एक वृत्त का केंद्र है। CP द्वारा बनने वाले वृत्त के लघु वृत्तखंड को छायांकित कीजिए।
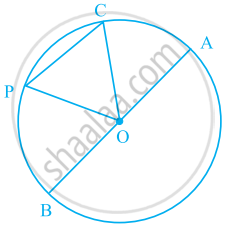
एक वृत्त की त्रिज्या 10 सेमी तथा जीवा की केंद्र से दूरी 6 सेमी है तो उस जीवा की लंबाई कितनी होगी?
