Advertisements
Advertisements
Question
AOB वृत्त का एक व्यास है तथा C वृत्त पर स्थित कोई बिंदु है। तब, AC2 + BC2 = AB2 है।
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण -
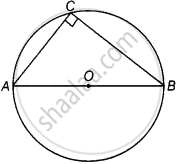
चूँकि, वृत्त का कोई भी व्यास वृत्त पर स्थित किसी भी बिंदु पर समकोण बनाता है।
यदि AOB एक वृत्त का व्यास है और C वृत्त पर एक बिंदु है, तो ΔACB, C पर समकोण है।
समकोण ΔACB में,
AC2 + BC2 = AB2 ...[पाइथागोरस प्रमेय का उपयोग करें]
APPEARS IN
RELATED QUESTIONS
वृत्त की सबसे बड़ी जीवा वृत्त का _____ होता है।
एक वृत्त, जिस तल पर स्थित है, उसे _______ भागों में विभाजित करता है।
संलग्न आकृति देखकर लिखिए:
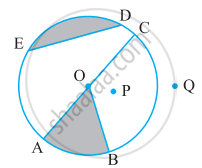
वृत का केंद्र
संलग्न आकृति देखकर लिखिए:

एक व्यास
क्या वृत का प्रत्येक जीवा उसका एक व्यास भी होती है?
किसी वृत्त का AD एक व्यास है और AB एक जीवा है। यदि AD = 34 cm, AB = 30 cm है, तो वृत्त के केंद्र से AB की दूरी है
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इस चतुर्भुज के परिगत वृत्त का एक व्यास है तथा ∠ADC = 140° है। तब, ∠BAC बराबर है
एक वृत्त की त्रिज्या `sqrt2` cm है। 2 cm लंबाई वाली जीवा द्वारा यह वृत्त दो वृत्त-खंडों में विभाजित किया जाता है। सिद्ध कीजिए कि इस जीवा द्वारा दीर्घ वृत्त-खंड के किसी बिंदु पर बना कोण 45° है।
चाँदे का प्रयोग किए बिना, दो न्यूनकोण और एक अधिक कोण खींचिए। इन कोणों की मापों का आकलन कीजिए। इनको चाँदे से मापिए और देखिए कि आपका आकलन कितना सही है।
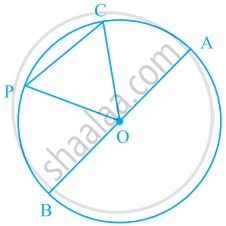
आकृति में O एक वृत्त का केंद्र है। वृत्त की सभी जीवाओं के नाम लिखिए।