Advertisements
Advertisements
प्रश्न
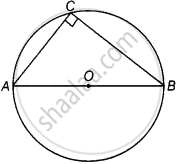
AOB वृत्त का एक व्यास है तथा C वृत्त पर स्थित कोई बिंदु है। तब, AC2 + BC2 = AB2 है।
विकल्प
सत्य
असत्य
उत्तर
यह कथन सत्य है।
स्पष्टीकरण -
चूँकि, वृत्त का कोई भी व्यास वृत्त पर स्थित किसी भी बिंदु पर समकोण बनाता है।
यदि AOB एक वृत्त का व्यास है और C वृत्त पर एक बिंदु है, तो ΔACB, C पर समकोण है।
समकोण ΔACB में,
AC2 + BC2 = AB2 ...[पाइथागोरस प्रमेय का उपयोग करें]
APPEARS IN
संबंधित प्रश्न
एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के _________ स्थित होता है।
केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखंड वृत्त की त्रिज्या होती है।
वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दो गुनी हो, वृत्त का व्यास है।
संलग्न आकृति देखकर लिखिए:
एक त्रिज्यखंड
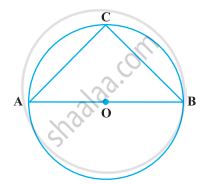
निम्नलिखित आकृति में, यदि AOB वृत्त का एक व्यास तथा AC = BC है, तो ∠CAB बराबर है
दो बिंदुओं A और B से होकर 3 cm त्रिज्या का एक वृत्त खींचा जा सकता है, यदि AB = 6 cm है।
आकृति में O एक वृत्त का केंद्र है। वृत्त की सभी त्रिज्याओं के नाम लिखिए।
एक वृत्त की त्रिज्या 10 सेमी तथा जीवा की केंद्र से दूरी 6 सेमी है तो उस जीवा की लंबाई कितनी होगी?
किसी वृत्त की जीवा की लंबाई 24 सेमी तथा केंद्र से जीवा 5 सेमी दूरी पर है तो वृत्त की त्रिज्या ज्ञात कीजिए?
किसी वृत्त की समांतर जीवाओं की लंबाई क्रमशः 6 सेमी तथा 8 सेमी है। उस वृत्त की त्रिज्या 5 सेमी हो तो उन जीवाओं के बीच दूरी कितनी होगी?
