Advertisements
Advertisements
प्रश्न
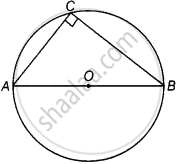
AOB वृत्त का एक व्यास है तथा C वृत्त पर स्थित कोई बिंदु है। तब, AC2 + BC2 = AB2 है।
पर्याय
सत्य
असत्य
उत्तर
यह कथन सत्य है।
स्पष्टीकरण -
चूँकि, वृत्त का कोई भी व्यास वृत्त पर स्थित किसी भी बिंदु पर समकोण बनाता है।
यदि AOB एक वृत्त का व्यास है और C वृत्त पर एक बिंदु है, तो ΔACB, C पर समकोण है।
समकोण ΔACB में,
AC2 + BC2 = AB2 ...[पाइथागोरस प्रमेय का उपयोग करें]
APPEARS IN
संबंधित प्रश्न
वृत्त का केन्द्र वृत्त के ______ में स्थित है।
एक चाप _______ होता है, जब इसके सिरे एक व्यास के सिरे हों।
वृत्तखंड एक चाप तथा ______ के बीच का भाग होता है।
संलग्न आकृति देखकर लिखिए:
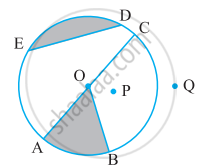
एक वृतखंड
कोई वृत खींचिए और निम्न को अंकित कीजिए:
-
उसका केंद्र
-
एक वृतखंड
-
एक त्रिज्या
-
उसके अभ्यंतर में एक बिंदु
-
एक व्यास
-
उसके बहिर्भाग में एक बिंदु
-
एक त्रिज्यखंड
- एक चाप
सत्य या असत्य बताइए:
वृत का केंद्र सदैव उसके अभ्यंतर में स्थित होता है।
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इस चतुर्भुज के परिगत वृत्त का एक व्यास है तथा ∠ADC = 140° है। तब, ∠BAC बराबर है
O और O' केंद्रों वाले दो सर्वांगसम वृत्त A और B दो बिंदुओं पर प्रतिच्छेद करते हैं। तब, ∠AOB = ∠AO'B हैं।
चाँदे का प्रयोग किए बिना, दो न्यूनकोण और एक अधिक कोण खींचिए। इन कोणों की मापों का आकलन कीजिए। इनको चाँदे से मापिए और देखिए कि आपका आकलन कितना सही है।
किसी O केंद्रवाले वृत्त की त्रिज्या 4 सेमी है। l(OP) = 4.2 सेमी हो तो बिंदु ‘P’ कहाँ होगा?
