Advertisements
Advertisements
प्रश्न
O और O' केंद्रों वाले दो सर्वांगसम वृत्त A और B दो बिंदुओं पर प्रतिच्छेद करते हैं। तब, ∠AOB = ∠AO'B हैं।
पर्याय
सत्य
असत्य
उत्तर
यह कथन सत्य है।
स्पष्टीकरण -
मान लीजिए O और O' केंद्र वाले सर्वांगसम वृत्त A और B पर प्रतिच्छेद करते हैं।
AB, O'A, O'B, OA और OB को मिलाइए।
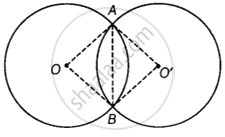
बिंदुओं को मिलाने पर हमें दो त्रिभुज अर्थात् OAB और O'AB प्राप्त होते हैं।
चूँकि दोनों वृत्त सर्वांगसम हैं, इसलिए ΔOAB और ΔO'AB में, हमारे पास :
OA = OA ...(दोनों वृत्तों की त्रिज्या समान होती है क्योंकि वृत्त सर्वांगसम होते हैं।)
OB = O’B ...(दोनों वृत्तों की त्रिज्या समान है क्योंकि वृत्त सर्वांगसम हैं।)
AB = AB ...(उभयनिष्ठ)
∴ SSS सर्वांगसमता नियम के अनुसार ΔOAB = ΔO'AB है।
∴ CPCT द्वारा, ∠AOB = ∠AO'B।
APPEARS IN
संबंधित प्रश्न
एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के _________ स्थित होता है।
एक चाप _______ होता है, जब इसके सिरे एक व्यास के सिरे हों।
वृत्तखंड एक चाप तथा ______ के बीच का भाग होता है।
वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दो गुनी हो, वृत्त का व्यास है।
संलग्न आकृति देखकर लिखिए:

एक व्यास
यदि AB = 12 cm, BC = 16 cm और AB रेखाखंड BC पर लंब है, तो A, B और C से होकर जाने वाले वृत्त की त्रिज्या है
यदि एक वृत्त PXAQBY की एक जीवा AB का लंब समद्विभाजक वृत्त को P और Q बिंदुओं पर प्रतिच्छेद करता है, तो सिद्ध कीजिए कि चाप PXA ≅ चाप PYB हैं।
O त्रिभुज ABC का परिकेंद्र है तथा D आधार BC का मध्य-बिंदु है। सिद्ध कीजिए कि ∠BOD = ∠A है।
निम्नलिखित आकृति में, ∠ACB = 40° है। ∠OAB ज्ञात कीजिए।
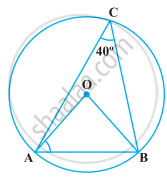
चाँदे का प्रयोग किए बिना, दो न्यूनकोण और एक अधिक कोण खींचिए। इन कोणों की मापों का आकलन कीजिए। इनको चाँदे से मापिए और देखिए कि आपका आकलन कितना सही है।
