Advertisements
Advertisements
Question
O और O' केंद्रों वाले दो सर्वांगसम वृत्त A और B दो बिंदुओं पर प्रतिच्छेद करते हैं। तब, ∠AOB = ∠AO'B हैं।
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण -
मान लीजिए O और O' केंद्र वाले सर्वांगसम वृत्त A और B पर प्रतिच्छेद करते हैं।
AB, O'A, O'B, OA और OB को मिलाइए।
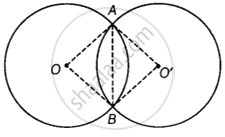
बिंदुओं को मिलाने पर हमें दो त्रिभुज अर्थात् OAB और O'AB प्राप्त होते हैं।
चूँकि दोनों वृत्त सर्वांगसम हैं, इसलिए ΔOAB और ΔO'AB में, हमारे पास :
OA = OA ...(दोनों वृत्तों की त्रिज्या समान होती है क्योंकि वृत्त सर्वांगसम होते हैं।)
OB = O’B ...(दोनों वृत्तों की त्रिज्या समान है क्योंकि वृत्त सर्वांगसम हैं।)
AB = AB ...(उभयनिष्ठ)
∴ SSS सर्वांगसमता नियम के अनुसार ΔOAB = ΔO'AB है।
∴ CPCT द्वारा, ∠AOB = ∠AO'B।
APPEARS IN
RELATED QUESTIONS
केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखंड वृत्त की त्रिज्या होती है।
वृत्त एक समतल आकृति है।
संलग्न आकृति देखकर लिखिए:
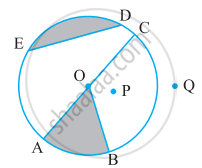
वृत का केंद्र
संलग्न आकृति देखकर लिखिए:
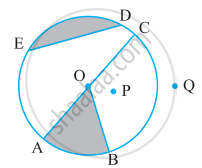
बहिर्भाग में एक बिंदु
क्या वृत का प्रत्येक जीवा उसका एक व्यास भी होती है?
निम्नलिखित आकृति में, यदि OA = 5 cm, AB = 8 cm तथा OD जीवा AB पर लंब है, तो CD बराबर है
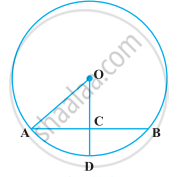
यदि AB = 12 cm, BC = 16 cm और AB रेखाखंड BC पर लंब है, तो A, B और C से होकर जाने वाले वृत्त की त्रिज्या है
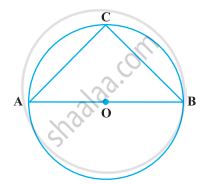
निम्नलिखित आकृति में, यदि AOB वृत्त का एक व्यास तथा AC = BC है, तो ∠CAB बराबर है
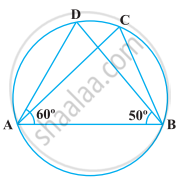
निम्नलिखित आकृति में, यदि ∠DAB = 60°, ∠ABD = 50° है, तो ∠ACB बराबर है
किसी O केंद्रवाले वृत्त की त्रिज्या 4 सेमी है। l(OP) = 4.2 सेमी हो तो बिंदु ‘P’ कहाँ होगा?
