Advertisements
Advertisements
प्रश्न
O और O' केंद्रों वाले दो सर्वांगसम वृत्त A और B दो बिंदुओं पर प्रतिच्छेद करते हैं। तब, ∠AOB = ∠AO'B हैं।
विकल्प
सत्य
असत्य
उत्तर
यह कथन सत्य है।
स्पष्टीकरण -
मान लीजिए O और O' केंद्र वाले सर्वांगसम वृत्त A और B पर प्रतिच्छेद करते हैं।
AB, O'A, O'B, OA और OB को मिलाइए।
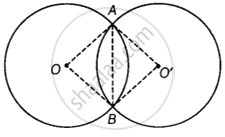
बिंदुओं को मिलाने पर हमें दो त्रिभुज अर्थात् OAB और O'AB प्राप्त होते हैं।
चूँकि दोनों वृत्त सर्वांगसम हैं, इसलिए ΔOAB और ΔO'AB में, हमारे पास :
OA = OA ...(दोनों वृत्तों की त्रिज्या समान होती है क्योंकि वृत्त सर्वांगसम होते हैं।)
OB = O’B ...(दोनों वृत्तों की त्रिज्या समान है क्योंकि वृत्त सर्वांगसम हैं।)
AB = AB ...(उभयनिष्ठ)
∴ SSS सर्वांगसमता नियम के अनुसार ΔOAB = ΔO'AB है।
∴ CPCT द्वारा, ∠AOB = ∠AO'B।
APPEARS IN
संबंधित प्रश्न
एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के _________ स्थित होता है।
संलग्न आकृति देखकर लिखिए:
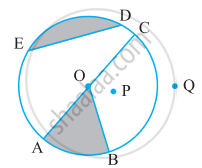
तीन त्रिज्याएँ
संलग्न आकृति देखकर लिखिए:
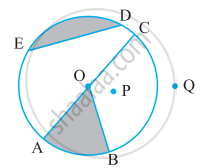
अभ्यंतर में दो बिंदु
संलग्न आकृति देखकर लिखिए:
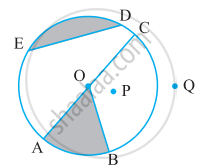
एक त्रिज्यखंड
कोई वृत खींचिए और निम्न को अंकित कीजिए:
-
उसका केंद्र
-
एक वृतखंड
-
एक त्रिज्या
-
उसके अभ्यंतर में एक बिंदु
-
एक व्यास
-
उसके बहिर्भाग में एक बिंदु
-
एक त्रिज्यखंड
- एक चाप
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इस चतुर्भुज के परिगत वृत्त का एक व्यास है तथा ∠ADC = 140° है। तब, ∠BAC बराबर है
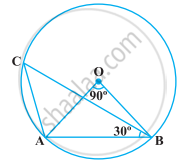
निम्नलिखित आकृति में, ∠AOB = 90° और ∠ABC = 30° है। तब, ∠CAO बराबर है :
O त्रिभुज ABC का परिकेंद्र है तथा D आधार BC का मध्य-बिंदु है। सिद्ध कीजिए कि ∠BOD = ∠A है।
किसी वृत्त की जीवा की लंबाई 24 सेमी तथा केंद्र से जीवा 5 सेमी दूरी पर है तो वृत्त की त्रिज्या ज्ञात कीजिए?
किसी O केंद्रवाले वृत्त की त्रिज्या 4 सेमी है। l(OP) = 4.2 सेमी हो तो बिंदु ‘P’ कहाँ होगा?
