Advertisements
Advertisements
प्रश्न
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इस चतुर्भुज के परिगत वृत्त का एक व्यास है तथा ∠ADC = 140° है। तब, ∠BAC बराबर है
विकल्प
80º
50º
40º
30º
उत्तर
50º
स्पष्टीकरण -
दिया गया है, ABCD एक चक्रीय चतुर्भुज है और ∠ADC = 140° है।
हम जानते हैं कि, चक्रीय चतुर्भुज में सम्मुख कोणों का योग 180° होता है।
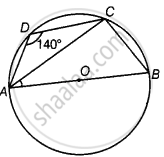
∠ADC + ∠ABC = 180°
⇒ 140° + ∠ABC = 180°
⇒ ∠ABC = 180° – 140°
∴ ∠ABC = 40°
चूँकि, ∠ACB अर्धवृत्त में एक कोण है।
∴ ∠ACB = 90°
∠ABC में, ∠BAC + ∠ACB + ∠ABC = 180° ...[त्रिभुज के कोण योग गुण द्वारा]
⇒ ∠BAC + 90° + 40° = 180°
⇒ ∠BAC = 180° – 130° = 50°
APPEARS IN
संबंधित प्रश्न
वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दो गुनी हो, वृत्त का व्यास है।
त्रिज्यखंड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
संलग्न आकृति देखकर लिखिए:
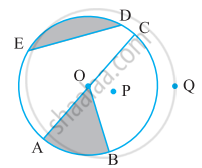
एक जीवा
संलग्न आकृति देखकर लिखिए:
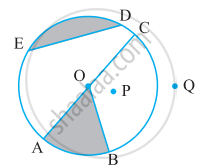
एक त्रिज्यखंड
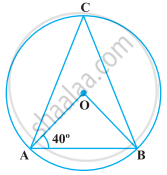
निम्नलिखित आकृति में, यदि ∠OAB = 40° है, तो ∠ACB बराबर है
O और O' केंद्रों वाले दो सर्वांगसम वृत्त A और B दो बिंदुओं पर प्रतिच्छेद करते हैं। तब, ∠AOB = ∠AO'B हैं।
O त्रिभुज ABC का परिकेंद्र है तथा D आधार BC का मध्य-बिंदु है। सिद्ध कीजिए कि ∠BOD = ∠A है।
आकृति में O एक वृत्त का केंद्र है। वृत्त की सभी जीवाओं के नाम लिखिए।
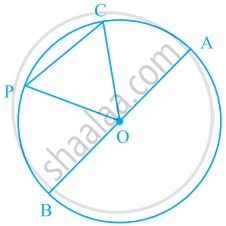
आकृति में O एक वृत्त का केंद्र है। एक ऐसी जीवा लिखिए, जो व्यास नहीं है।
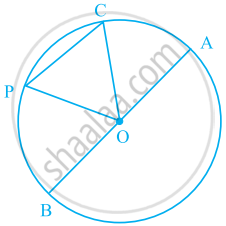
त्रिभुज के तीनों कोणों के समद्विभाजक संगामी होते हैं। उनके संगामी बिंदु को क्या कहते हैं?
