Advertisements
Advertisements
Question
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इस चतुर्भुज के परिगत वृत्त का एक व्यास है तथा ∠ADC = 140° है। तब, ∠BAC बराबर है
Options
80º
50º
40º
30º
Solution
50º
स्पष्टीकरण -
दिया गया है, ABCD एक चक्रीय चतुर्भुज है और ∠ADC = 140° है।
हम जानते हैं कि, चक्रीय चतुर्भुज में सम्मुख कोणों का योग 180° होता है।
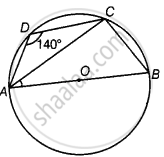
∠ADC + ∠ABC = 180°
⇒ 140° + ∠ABC = 180°
⇒ ∠ABC = 180° – 140°
∴ ∠ABC = 40°
चूँकि, ∠ACB अर्धवृत्त में एक कोण है।
∴ ∠ACB = 90°
∠ABC में, ∠BAC + ∠ACB + ∠ABC = 180° ...[त्रिभुज के कोण योग गुण द्वारा]
⇒ ∠BAC + 90° + 40° = 180°
⇒ ∠BAC = 180° – 130° = 50°
APPEARS IN
RELATED QUESTIONS
वृत्त की सबसे बड़ी जीवा वृत्त का _____ होता है।
एक चाप _______ होता है, जब इसके सिरे एक व्यास के सिरे हों।
वृत्त एक समतल आकृति है।
सत्य या असत्य बताइए:
वृत का केंद्र सदैव उसके अभ्यंतर में स्थित होता है।
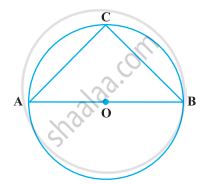
निम्नलिखित आकृति में, यदि AOB वृत्त का एक व्यास तथा AC = BC है, तो ∠CAB बराबर है
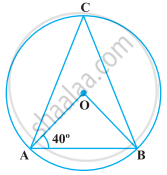
निम्नलिखित आकृति में, यदि ∠OAB = 40° है, तो ∠ACB बराबर है
O और O' केंद्रों वाले दो सर्वांगसम वृत्त A और B दो बिंदुओं पर प्रतिच्छेद करते हैं। तब, ∠AOB = ∠AO'B हैं।
AOB वृत्त का एक व्यास है तथा C वृत्त पर स्थित कोई बिंदु है। तब, AC2 + BC2 = AB2 है।
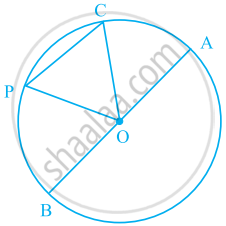
आकृति में O एक वृत्त का केंद्र है। एक ऐसी जीवा लिखिए, जो व्यास नहीं है।
त्रिभुज के तीनों कोणों के समद्विभाजक संगामी होते हैं। उनके संगामी बिंदु को क्या कहते हैं?
