Advertisements
Advertisements
प्रश्न
निम्नलिखित आकृति में, ∠AOB = 90° और ∠ABC = 30° है। तब, ∠CAO बराबर है :
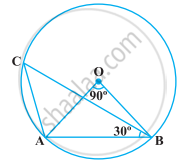
विकल्प
30⁰
45⁰
90⁰
60⁰
उत्तर
60⁰
स्पष्टीकरण -

चूँकि, किसी चाप द्वारा केन्द्र पर बनाया गया कोण, वृत्त के शेष भाग पर किसी भी बिंदु पर बनाए गए कोण का दोगुना होता है।
∴ ∠AOB = 2∠ACB
साथ ही, AO = OB ...[एक ही वृत्त की त्रिज्याएँ]
अब, ΔOAB में, ∠OAB + ∠ABO + ∠BOA = 180° ...[त्रिभुज के कोणों का योग 180° होता है।]
∴ ∠OAB + ∠OAB + 90° = 180° ...[(i) से]
साथ ही, ΔACB में, ∠ACB + ∠CBA + ∠CAB = 180° ...[त्रिभुज के कोणों का योग 180° होता है।]
∴ 45° + 30° + ∠CAB = 180° ...[∵ ∠ABC = 30°]
चूँकि, ∠CAO + ∠OAB = ∠CAB
APPEARS IN
संबंधित प्रश्न
वृत्तखंड एक चाप तथा ______ के बीच का भाग होता है।
एक वृत्त में समान लंबाई की परिमित जीवाएँ होती हैं।
वृत्त एक समतल आकृति है।
सत्य या असत्य बताइए:
वृत का केंद्र सदैव उसके अभ्यंतर में स्थित होता है।
यदि AB = 12 cm, BC = 16 cm और AB रेखाखंड BC पर लंब है, तो A, B और C से होकर जाने वाले वृत्त की त्रिज्या है
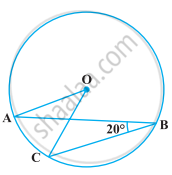
निम्नलिखित आकृति में, यदि ∠ABC = 20° है, तो ∠AOC बराबर है
निम्नलिखित आकृति में, BC वृत्त का व्यास है तथा ∠BAO = 60° है। तब, ∠ADC बराबर है
दो बिंदुओं A और B से होकर 3 cm त्रिज्या का एक वृत्त खींचा जा सकता है, यदि AB = 6 cm है।
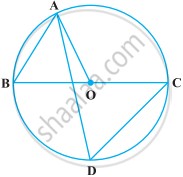
O त्रिभुज ABC का परिकेंद्र है तथा D आधार BC का मध्य-बिंदु है। सिद्ध कीजिए कि ∠BOD = ∠A है।
किसी वृत्त की जीवा की लंबाई 24 सेमी तथा केंद्र से जीवा 5 सेमी दूरी पर है तो वृत्त की त्रिज्या ज्ञात कीजिए?
