Advertisements
Advertisements
प्रश्न
एक तेल कारखाने में दो डिपो A तथा B हैं, जिनकी क्षमताएँ क्रमशः 7000 लिटर और 4000 लिटर की हैं। कारखाने द्वारा तीन पेट्रोल पंपों D, E और F के लिए आपूर्ति करनी है, जिनकी आवश्यकताएँ क्रमशः 4500 लिटर, 3000 लिटर और 3500 लिटर की है। डिपो से पेट्रोल पंपों की दूरियाँ (km में) निम्नांकित सारणी के अनुसार है:
| दूरियाँ (km में) | ||
| को/से | A | B |
| D | 7 | 3 |
| E | 6 | 4 |
| F | 3 | 2 |
यह मानते हुए कि परिवहन व्यय प्रति 10 लिटर पर प्रति किलोमीटर 1 रुपया है, ज्ञात कीजिए कि कैसी आपूर्ति योजना अपनाई जाए, जिससे परिवहन व्यय का न्यूनतमीकरण हो जाए? न्यूनतम व्यय क्या है?
उत्तर
बता दें कि ए और पेट्रोल पंपों से एक्स और वाई लीटर तेल की आपूर्ति की जाती है, डी और ई। तब, (7000 - Xy) ए से पेट्रोल पंप एफ को आपूर्ति की जाएगी। पेट्रोल पंप डी पर आवश्यकता 4500 एल है। चूंकि एक्स एल डिपो ए से परिवहन किया जाता है, शेष (4500-एक्स) एल को पेट्रोल पंप बी से ले जाया जाएगा | इसी तरह, (3000 - वाई) एल और 3500 - (7000 - x - y) = (x + y - 3500) एल क्रमशः डिपो बी से पेट्रोल पंप ई और एफ तक पहुँचाया जाए। दी गई समस्या का चित्रण निम्न प्रकार से किया जा सकता है।
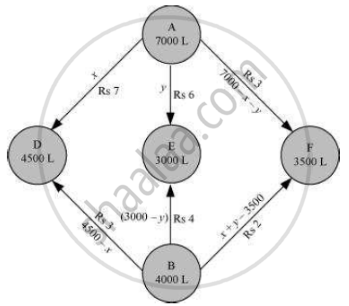
x ≥ 0, y ≥ 0 and (7000 - x - y) ≥ 0
x ≥ 0, y ≥ 0 and x + y ≤ 7000
10 एल पेट्रोल = रे 1 के परिवहन की लागत
4500 - x ≥ 0, 3000 - y ≥ 0 and x + y - 3500 ≥ 0
x ≤ 4500, y ≤ 3000 and x + y ≤ 3500
1 एल पेट्रोल की ढुलाई की लागत = 10 इसलिए, कुल परिवहन लागत द्वारा दी गई है,
Z = 7x/10x + 6y/10 + 3(7000 - x - y)/10 + 3(4500 - x)/10 + 4(3000 - y)/10 + 2(x + y - 3500)/10
= 0.3x + 0.1y + 3950
मस्या निन्मानुसार बनाई जा सकती है | कम से कम z = 0.3x + 0.1y + 3950 .......(1)
बाधाओं के अधीन,
बाधाओं द्वारा निर्धारित संभाव्य क्षेत्र इस प्रकार है |
x + y ≤ 7000 ..........(2)
x ≤ 4500 .......(3)
y ≤ 3000 ........(4)
x + y ≥ 3500 ........(5)
x, y ≥ 0 .......(6)
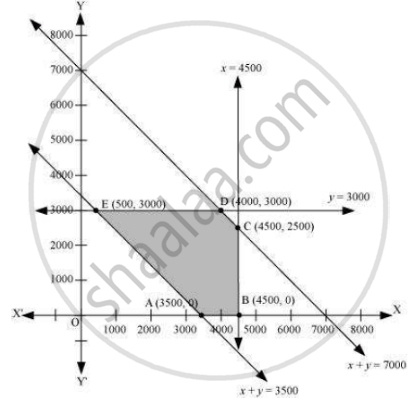
संभव क्षेत्र के कोने बिंदु A(3500, 0), B(4500, 0), C(4500, 2500), D(4000, 3000) और E(500, 3000) हैं। इन कोने बिंदुओं पर z का मान इस प्रकार है।
| Corner point | z = 0.3x + 0.1y + 3950 | |
| A(3500, 0) | 5000 | |
| B(4500, 0) | 5300 | |
| C(4500, 2500) | 5550 | |
| D(4000, 3000) | 5450 | |
| E(500, 3000) | 4400 | → Minimum |
Z का न्यूनतम मान 4400 पर (500, 3000) है। इस प्रकार, डिपो A से आपूर्ति किया जाने वाला तेल क्रमशः 500 L, 3000 L और 3500 L है और डिपो B से 4000 L, O L, और O L क्रमशः पेट्रोल D, E और F से पंप करता है। न्यूनतम परिवहन लागत 4400 रुपये है।
APPEARS IN
संबंधित प्रश्न
रेशमा दो प्रकार के भोज्य P और Q को इस प्रकार मिलाना चाहती है कि मिश्रण में विटामिन अवयवों में 8 मात्रक विटामिन A तथा 11 मात्रक विटामिन B हों | भोज्य P की लागत Rs 60/kg और भोज्य Q की लागत Rs 80/kg है | भोज्य P में 3 मात्रक/kg विटामिन A और 5 मात्रक/kg विटामिन B है जबकि भोज्य Q में 4 मात्रक/kg विटामिन A और 2 मात्रक/kg विटामिन है | मिश्रण की न्यूनतम लागत ज्ञात कीजिए |
एक प्रकार के केक को 200 g आटा तथा 25 g वसा (fat) की आवश्यकता होती है तथा दूसरी प्रकार के केक के लिए 100 g आटा तथा 50 g वसा की आवश्यकता होती है | केकों की अधिकतम संख्या बताओ जो 5 किलो आटे तथा 1 किलो वसा से बन सकते हैं, यह मान लिया गया है कि केकों को बनाने के लिए अन्य पदार्थों की कमी नहीं रहेगी |
एक कुटीर उद्योग निर्माता पैडेस्टल लैंप और लकड़ी के शेड बनाता है | प्रत्येक के निर्माण में एक रगड़ने/काटने और एक स्प्रेयर की आवश्यकता पड़ती है | एक लैंप के निर्माण में 2 घंटे रगड़ने/काटने और 3 घंटे स्प्रेयर की आवश्यकता होती है, जबकि एक शेड के निर्माण में 1 घंटा रगड़ने/काटने और 2 घंटे स्प्रेयर की आवश्यकता होती है | स्प्रेयर की मशीन प्रतिदिन अधिकतम 20 घंटे और रगड़ने/काटने की मशीन प्रतिदिन अधिकतम 12 घंटे के लिए उपलब्ध है | एक लैंप की बिक्री पर Rs 5 और एक शेड की बिक्री पर Rs 3 का लाभ होता है | यह मानते हुए कि सभी निर्मित लैंप और शेड बिक जाते है, तो बताइए वह निर्माण की प्रतिदिन कैसी योजना बनाए कि लाभ अधिकतम हो?
एक कंपनी प्लाईवुड के अनूठे स्मृति चिन्ह का निर्माण करती है। A प्रकार के प्रति स्मृति चिन्ह के निर्माण में 5 मिनट काटने और 10 मिनट जोड़ने में लगते हैं। B प्रकार के प्रति स्मृति चिन्ह के लिए 8 मिनट काटने और 8 मिनट जोड़ने में लगते हैं। दिया गया है कि काटने के लिए कुल समय 3 घंटे 20 मिनट तथा जोड़ने के लिए 4 घंटे उपलब्ध हैं। प्रत्येक A प्रकार स्मृति चिन्ह पर Rs 5 और प्रत्येक B प्रकार के स्मृति चिन्ह पर Rs 6 का लाभ होना है। ज्ञात कीजिए कि लाभ के अधिकतमीकरण के लिए प्रत्येक प्रकार के कितने-कितने स्मृति चिन्हों का कंपनी द्वारा निर्माण होना चाहिए?
एक सौदागर दो प्रकार के निजी कंप्यूटर-एक डेस्कटॉप नमूना और दूसरा पोर्टेबल नमूना, जिनकी कीमतें क्रमशः Rs 25,000 और Rs 40,000 होगी, बेचने की योजना बनाता है | वह अनुमान लगाता है कि कंप्यूटरों की कुल मासिक माँग 250 नगों से अधिक नहीं होगी | प्रत्येक प्रकार के कंप्यूटरों के नगों की संख्या ज्ञात कीजिए जिसे सौदागर अधिकतम लाभ प्राप्त करने के लिए संग्रह करें यदि उसके पास निवेश के लिए Rs 70 लाख से अधिक नहीं है और यदि डेस्कटॉप नमूने पर उसका लाभ Rs 4500 और पोर्टेबल नमूने पर Rs 5000 लाभ हो |
एक भोज्य पदार्थ में कम से कम 80 मात्रक विटामिन A और 100 मात्रक खनिज होना चाहिए। दो प्रकार के भोज्य F1 और F2 उपलब्ध हैं। भोज्य F1 की लागत Rs 4 प्रति मात्रक और F2 की लागत Rs 5 प्रति मात्रक है। भोज्य F1 की एक इकाई में कम से कम ३ मात्रक विटामिन A और 4 मात्रक खनिज है। F2 की प्रति इकाई में कम से कम 6 मात्रक विटामिन A और 3 मात्रक खनिज हैं। इसको एक रैखिक प्रोग्रामन समस्या के रूप में सूत्रबध्द कीजिए। उस आहार का न्यूनतम मूल्य ज्ञात कीजिए, जिसमें इन दो भोज्यों का मिश्रण है और उसमें न्यूनतम पोषक तत्व हैं।
दो प्रकार के उर्वरक F1 और F2 है | F1 में 10% नायट्रोजन और 6% फास्फोरिक अम्ल है। तथा F2 में 5% नाइट्रोजन तथा 10% फास्फोरिक अम्ल है। मिट्टी की स्थितिओं का परिक्षण करने के पश्चात् एक किसान पाता है कि उसे अपनी फसल के लिए 14 kg नाइट्रोजन और 14 kg फास्फोरिक अम्ल की आवश्यकता है। यदि F1 की कीमत Rs 6/kg और F2 की कीमत Rs 5/kg है, प्रत्येक प्रकार का कितना उर्वरक उपयोग के लिए चाहिए ताकि न्यूनतम मूल्य पर वांछित पोषक तत्व मिल सके। न्यूनतम लागत क्या है।
निम्नलिखित असमीकरण निकायः 2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 से निर्धारित सुसंगत क्षेत्र के कोनीय बिंदु: (0, 0), (5, 0), (3, 4) और (0, 5) है। मानाकि Z = px + qy, जहाँ p, q > 0 p तथा q के लिए निम्नलिखित में कौन प्रतिबंध उचित है ताकि Z का अधिकतम (3, 4) और (0, 5) दोनों पर घटित होता है-
एक खिलौना कंपनी, A और B दो प्रकार की गुड़ियों का निर्माण करती है। मार्किट परीक्षणों तथा उपलब्ध संसाधनों से संकेत मिलता है कि सम्मिलित उत्पादन स्तर प्रति सप्ताह 1200 गुड़ियों से अधिक नहीं होना चाहिए और B प्रकार की गुड़ियों की अधिक से अधिक माँग A प्रकार की गुड़ियों की आधी है। इसके अतिरिक्त A प्रकार गुड़ियों का उत्पादन स्तर दूसरे प्रकार की गुड़ियों के उत्पादन स्तर के तीन गुने से 600 नग अधिक है। यदि कंपनी A और B प्रत्येक गुड़ियों पर क्रमशः Rs 12 और Rs 16 का लाभ कमाती है, लाभ का अधिकतमीकरण करने के लिए प्रत्येक के कितने नगों का साप्ताहिक उत्पादन करना चाहिए।
उपरोक्त प्रश्न 8 पर ध्यान दीजिए | यदि उत्पादक बाग में मिलाई जाने वाली नाइट्रोजन की मात्रा का अधिकतमीकरण चाहता है तो मिश्रण के कितने थैलों को मिलाया जाना चाहिए? मिलाई जाने वाली नाइट्रोजन की अधिकतम मात्रा क्या है?
एक फल उत्पादक अपने बाग में दो प्रकार के खादों P ब्रांड और Q ब्रांड का उपयोग क्र सकता है | मिश्रण के प्रत्येक थैले में नाइट्रोजन, फास्फोरिक अम्ल, पोटाश और क्लोरीन की मात्रा (kg में) सारणी में दिया गया है | परिक्षण संकेत देते है कि बाग को कम से कम 250 kg फास्फोरिक अम्ल, कम से कम 270 kg पोटाश और क्लोरीन की अधिक से अधिक 310 kg की आवश्यकता है |
उदाहरण 9 पर ध्यान कीजिए | आहार में विटामिन A की मात्रा का अधिकतमीकरण करने के लिए प्रत्येक भोज्य के कितने पैकेटों का उपयोग होना चाहिए? आहार में विटामिन A की अधिकतम मात्रा क्या है?
एक किसान दो प्रकार के चारे P और Q को मिलाता (मिश्रण) है। P प्रकार के चारे, जिसका मूल्य Rs 250 प्रति थैला जोकि पोषक तत्व A के 3 मात्रक, तत्व B के 2.5 मात्रक और तत्व C के 2 मात्रक रखता है जबकि Q प्रकार का चारा जिसका मूल्य Rs 200 प्रति थैला है, पोषक तत्व A का 1.5 मात्रक, तत्व B का 11.25 मात्रक और तत्व C के तीन मात्रक रखता है। पोषक तत्वों A, B और C की न्यूनतम आवश्यकताएँ क्रमशः 18 मात्रक, 45 मात्रक और 24 मात्रक हैं। प्रत्येक प्रकार के थैलों की संख्या ज्ञात कीजिए ताकि मिश्रण के प्रत्येक थैले का मूल्य न्यूनतम हो? मिश्रण के प्रत्येक थैले का न्यूनतम मूल्य क्या है?
एक निर्माता दो प्रकार के खिलौने A और B बनाता है। इस उदेश्य के लिए निर्माण में तीन मशीनों की आवश्यकता पड़ती है और प्रत्येक प्रकार के खिलौने के निर्माण के लिए लगा समय (मिनटों में) निम्नलिखित है।
| खिलौने के प्रकार | मशीन | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
प्रत्येक मशीन अधिकतम 6 घंटे प्रतिदिन के लिए उपलब्ध है। यदि A प्रकार के खिलौने की बिक्री पर Rs 7.50 लाभ और B प्रकार के खिलौने पर Rs 5 का लाभ हो तो दर्शाइए कि अधिकतम लाभ कमाने के लिए प्रतिदिन A प्रकार के 15 खिलौने और B प्रकार 30 खिलौने निर्मित होने चाहिए।
एक हवाई जहाज अधिकतम 200 यात्रियों को यात्रा करा सकता है। प्रत्येक प्रथम श्रेणी के टिकट पर Rs 1000 और सस्ते श्रेणी के टिकट पर Rs 600 का लाभ कमाया जा सकता है। एयरलाइन कम से कम 20 सीटें प्रथम श्रेणी के लिए आरक्षित करती है। तथापि प्रथम श्रेणी की अपेक्षा कम से कम 4 गुने यात्री सस्ती श्रेणी के टिकट से यात्रा करने को वरीयता देते हैं। ज्ञात कीजिए कि प्रत्येक के कितने-कितने टिकट बेचे जाएँ ताकि लाभ का अधिकतमीकरण हो? अधिकतम लाभ कितना है?
दो अन्न भंडारों A और B की भंडारण क्षमता क्रमशः 100 क्विंटल और 50 क्विंटल है। उन्हें तीन राशन की दुकानों D, E और F पर अन्न उपलब्ध कराना पड़ता है, जिनकी आवश्यकताएँ क्रमशः 60, 50 और 40 क्विंटल हैं।
भंडारों से दुकानों को प्रति क्विंटल परिवहन व्यय निम्न सारणी के अनुसार है:
| प्रति क्विंटल परिवहन व्यय (रुपयों में) | ||
| को/से | A | B |
| D | 6 | 4 |
| E | 3 | 2 |
| F | 2.50 | 3 |
परिवहन व्यय के न्यूनतमीकरण के लिए आपूर्ति का परिवहन कैसे किया जाए? न्यूनतम परिवहन मूल्य क्या है?
