Advertisements
Advertisements
प्रश्न
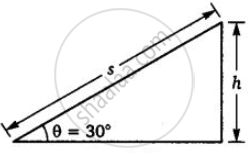
एक ठोस गोला, भिन्न नति के दो आनत तलों पर एक ही ऊँचाई से लुढ़कने दिया जाता है।
- क्या वह दोनों बार समान चाल से तली में पहुँचेगा?
- क्या उसको एक तल पर लुढ़कने में दूसरे से अधिक समय लगेगा?
- यदि हाँ, तो किस पर और क्यों?
उत्तर
- θ झुकाव कोण तथा h ऊँचाई के आनत तल पर लुढ़कने वाले सममित पिण्ड का पृथ्वी तल पर पहुँचने पर वेग ν हो तो –
`"ν"^2 = (2 "gh")/(1 + ("K"^2/"R"^2))`
जहाँ R = वस्तु की त्रिज्या तथा K = घूर्णन त्रिज्या
परन्तु गोले के लिए, `"MK"^2 = 2/5 "MR"^2 ⇒ "K"^2/"R"^2 = 2/5`
अतः `"ν"^2 = (2 "gh")/(1 + (2/5))` या
`"ν"^2 = 10/7 "gh"`
यहाँ पर स्पष्ट है कि गोले को तली पर पहुँचने का वेग आनत तल के झुकाव कोण 8 पर निर्भर नहीं करता, अतः गोला दोनों आनत तलों की तली पर समान चाल से पहुँचेगा। - यदि आनत तल की लम्बाई s हो तथा गोले द्वारा तली तक पहुँचने में लिया गया समय t हो तो –
`"s" = 1/2 "αt"^2 => "t" = sqrt((2"s")/"α")`
गोले का त्वरण, α = `("g" "sin" θ)/(1 + "K"^2/"R"^2) = ("g" "sin" θ)/(1 + 2/5) = 5/7 "g" "sin" θ`
परन्तु चित्र से, `"s" = "h"/("sin" θ)` ∴ समय, `"t" = sqrt((2 xx "h" // "sin" θ)/((5 "g" "sin" θ)//7))`
अथवा `"t" =[sqrt((14"h")/(5"g"))] xx 1/("sin" θ) => "t" ∝ 1/("sin" θ)`
चूँकि लिया गया समय आनत तल के झुकाव कोण पर निर्भर करता है, अतः दोनों तलों पर लुढ़कने का समय भिन्न-भिन्न होगा। - चूंकि t α 1/sin θ तथा 8 का मान बढ़ने से sin θ का मान बढ़ता है।
अतः θ के कम मान के लिए sin θ का मान कम होने के कारण t का मान अधिक होगा अर्थात् कम ढाल वाले तल पर लुढ़कने में लिया गया समय अधिक होगा।
APPEARS IN
संबंधित प्रश्न
2 m त्रिज्या के एक वलय (छल्ले) का भार 100 kg है। यह एक क्षैतिज फर्श पर इस प्रकार लोटनिक गति करता है कि इसके द्रव्यमान केन्द्र की चाल 20 cm/s हो। इसको रोकने के लिए कितना कार्य करना होगा ?
सूत्र `"ν"^2 = (2 "gh")/((1 + "k"^2//"R"^2))` को गतिकीय दृष्टि (अर्थात् बलों तथा बल-आघूर्णों विचार) से व्युत्पन्न कीजिए। जहाँ ν लोटनिक गति करते पिंड (वलय, डिस्क, बेलन या गोला) का आनत तल की तली में वेग है। आनत तल पर h वह ऊँचाई है जहाँ से पिण्ड गति प्रारंभ करता है। K सममित अक्ष के परितः पिंड की घूर्णन त्रिज्या है और R पिंड की त्रिज्या है।
अपने अक्ष पर ω0 कोणीय चाल से घूर्णन करने वाली किसी चक्रिका को धीरे से (स्थानान्तरीय धक्का दिए बिना) किसी पूर्णतः घर्षणरहित मेज पर रखा जाता है। चक्रिका की त्रिज्या R , है। चित्र में दर्शाई चक्रिका के बिंदुओं A, B तथा C पर रैखिक वेग क्या हैं? क्या यह चक्रिका चित्र में दर्शाई दिशा में लोटनिक गति करेगी?
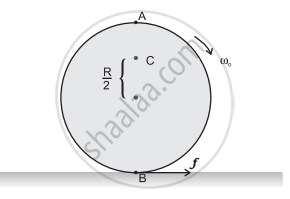
स्पष्ट कीजिए कि चित्र में अंकित दिशा में चक्रिका की लोटनिक गति के लिए घर्षण होना आवश्यक क्यों है?
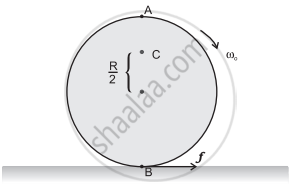
- B पर घर्षण बल की दिशा तथा परिशुद्ध लुढ़कन आरंभ होने से पूर्व घर्षणी बल-आघूर्ण की दिशा क्या है?
- परिशुद्ध लोटनिक गति आरंभ होने के पश्चात् घर्षण बल क्या है?
10 cm त्रिज्या की कोई ठोस चक्रिका तथा इतनी ही त्रिज्या का कोई छल्ला किसी क्षतिज मेज पर एक ही क्षण 10 π rad s-1 की कोणीय चाल से रखे जाते हैं। इनमें से कौन पहले लोटनिक गति आरंभ कर देगा। गतिज घर्षण गुणांक µk =0.2।
10 kg द्रव्यमान तथा 15 cm त्रिज्या का कोई सिलिंडर किसी 30° झुकाव के समतल पर परिशुद्धतः लोटनिक गति कर रहा है। स्थैतिक घर्षण गुणांक µs = 0.25 है।
- सिलिंडर पर कितना घर्षण बल कार्यरत है?
- लोटन की अवधि में घर्षण के विरुद्ध कितना कार्य किया जाता है?
- यदि समतल के झुकाव θ में वृद्धि कर दी जाए तो के किस मान पर सिलिंडर परिशुद्धतः लोटनिक गति करने की बजाय फिसलना आरंभ कर देगा?
नीचे दिए गए प्रकथन को ध्यानपूर्वक पढिए तथा कारण सहित उत्तर दीजिए कि सत्य है या असत्य?
लोटनिक गति करते समय घर्षण बल उसी दिशा में कार्यरत होता है जिस दिशा में पिण्ड का द्रव्यमान केंद्र गति करता है।
नीचे दिए गए प्रकथन को ध्यानपूर्वक पढिए तथा कारण सहित उत्तर दीजिए कि सत्य है या असत्य?
लोटनिक गति करते समय संपर्क बिंदु की तात्क्षणिक चाल शून्य होती है।
नीचे दिए गए प्रकथन को ध्यानपूर्वक पढिए तथा कारण सहित उत्तर दीजिए कि सत्य है या असत्य?
परिशुद्ध लोटनिक गति के लिए घर्षण के विरुद्ध किया गया कार्य शून्य होता है।
नीचे दिए गए प्रकथन को ध्यानपूर्वक पढिए तथा कारण सहित उत्तर दीजिए कि सत्य है या असत्य?
किसी पूर्णतः घर्षणरहित आनत समतल पर नीचे की ओर गति करते पहिये की गति फिसलन गति (लोटनिक गति नहीं) होगी।
