Advertisements
Advertisements
प्रश्न
एक व्यक्ती एका मंदिरापासून 50 मी. अंतरावर उभा आहे. त्या व्यक्तीने मंदिराच्या कळसाकडे पाहिले असता 45° मापाचा उन्नत कोन तयार होतो. तर त्या मंदिराची उंची किती?
उत्तर
समजा, आकृतीत AB ही मंदिराची उंची आहे.
C या ठिकाणी व्यक्ती उभी आहे.
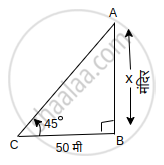
AB = x मी
BC = 50 मी
उन्नत कोन ∠CAB = θ = 45°
ΔABC मध्ये, ∠B = 90°
tanθ = `"AB"/"BC"`
tan45° = `x/50`
∴ `1 = x/50` ...........[tan45° = 1]
∴ x = 50 मी
∴ मंदिराची उंची 50 मी आहे.
APPEARS IN
संबंधित प्रश्न
दीपगृहावरून एका जहाजाकडे पाहताना 60° मापाचा अवनत कोन होतो. जर दीपगृहाची उंची 90 मी असेल तर ते जहाज दीपगृहापासून किती अंतरावर आहे? (`sqrt3` = 1.73)
12 मी रुंदीच्या रस्त्याच्या दुतर्फा समोरासमोर दोन इमारती आहेत. त्यांपैकी एकीची उंची 10 मी असून तिच्या छतावरून दुसरीच्या छताकडे पाहिले असता उन्नत कोन 60° मापाचा होतो, तर दुसऱ्या इमारतीची उंची किती?
जेव्हा आपण क्षितीजसमांतर रेषेच्या वरच्या दिशेने पाहतो, तेव्हा ______ कोन होतो.
15 मी रुंदीच्या रस्त्याच्या दुतर्फा समोरासमोर दोन इमारती आहेत. त्यांपैकी एकीची उंची 12 मी असून तिच्या छतावरुन दुसरीच्या छताकडे पाहिले असता उन्नत कोन 30° चा होतो, तर त्या इमारतीची उंची किती ?
`(cos(90 - "A"))/(sin "A") = (sin(90 - "A"))/(cos "A")` = हे सिद्ध करा.
जर tan θ = `9/40`, तर sec θ ची किंमत काढण्यासाठी खालील कृती पूर्ण करा.
कृती: sec2θ = 1 + `square` ......[त्रि. नित्य समीकरण]
sec2θ = 1 + `square^2`
sec2θ = 1 + `square`
sec θ = `square`
∆ABC मध्ये, cos C = `12/13` असून BC = 24, तर AC = ?
जर sin A = `3/5` तर 4 tan A + 3 sin A = 6 cos A दाखवा.
जर sec A = `x + 1/(4x)`, sec A + tan A = 2x किंवा `1/(2x)` हे दाखवा.
∆ABC मध्ये, `sqrt(2)` AC = BC, sin A = 1, sin2A + sin2B + sin2C = 2, तर ∠A = ? , ∠B = ?, ∠C = ?
