Advertisements
Advertisements
प्रश्न
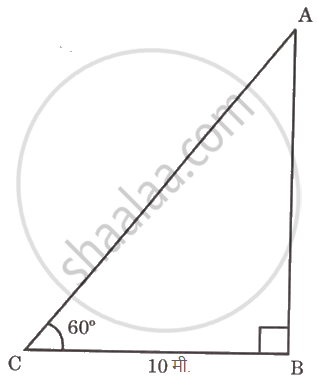
एका झाडाच्या बुंध्यापासून 10 मी. अंतरावर असणाऱ्या निरीक्षकास झाडाच्या शेंड्याकडे पाहताना 60° मापाचा उन्नत कोन करावा लागतो. तर झाडाची उंची काढण्यासाठी खालील कृती पूर्ण करा. `(sqrt3 = 1.73)`
कृती:
वरील आकृतीमध्ये, C बिंदूजवळ निरीक्षक असून AB हे झाड आहे. AB = h = झाडाची उंची, निरीक्षकाचे झाडापासूनचे अंतर BC = 10 मी., उन्नत कोन (θ) = ∠BCA = 60°.
आकृतीवरून,
tan θ = `square/("BC")` ...(I)
tan 60° = `square` ...(II)
`("AB")/("BC") = sqrt3` ...((I) व (II) वरून)
AB = BC × `sqrt3` = `10sqrt3`
AB = 10 × 1.73 = `square`
∴ झाडाची उंची `square` मी. आहे.
उत्तर
वरील आकृतीमध्ये, C बिंदूजवळ निरीक्षक असून AB हे झाड आहे. AB = h = झाडाची उंची, निरीक्षकाचे झाडापासूनचे अंतर BC = 10 मी., उन्नत कोन (θ) = ∠BCA = 60°.
आकृतीवरून,
tan θ = \[\frac{\boxed{\text{AB}}}{\text{BC}}\] ...(I)
tan 60° = \[\boxed{\sqrt{3}}\] ...(II)
`("AB")/("BC") = sqrt3` ...((I) व (II) वरून)
AB = BC × `sqrt3` = `10sqrt3`
AB = 10 × 1.73 = \[\boxed{17.3}\]
∴ झाडाची उंची \[\boxed{17.3}\] मी. आहे.
