Advertisements
Advertisements
प्रश्न
Explain the horizontal oscillations of a spring.
उत्तर
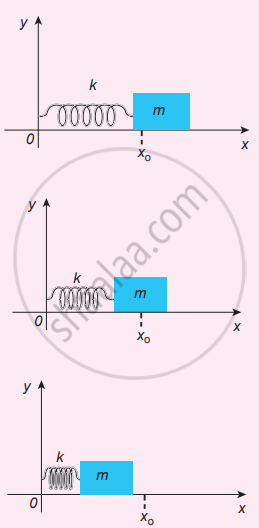
Horizontal oscillations of a spring-mass system: Consider a system containing a block of mass m attached to a massless spring with stiffness constant or force constant or spring constant k placed on a smooth horizontal surface (frictionless surface) as shown in the figure. Let x0 be the equilibrium position or mean position of mass m when it is left undisturbed. Suppose the mass is displaced through a small displacement x towards right from its equilibrium position and then released, it will oscillate back and forth about its mean position Let F be the restoring force (due to stretching of the spring) which is proportional to the amount of displacement of the block. For one dimensional motion, mathematically, we have
`"F" ∝ "x"`
F = −kx .................(1)
where negative sign implies that the restoring force will always act opposite to the direction of the displacement. This equation is called Hooke’s law. Notice that, the restoring force is linear with the displacement (i.e., the exponent of force and displacement are unity). This is not always true; in case if we apply a very large stretching force, then the amplitude of oscillations becomes very large (which means, force is proportional to displacement containing higher powers of x) and therefore, the oscillation of the system is not linear and hence, it is called non-linear oscillation. We restrict ourselves only to linear oscillations throughout our discussions, which means Hooke’s law is valid (force and displacement have a linear relationship).
From Newton’s second law, we can write the equation for the particle executing simple harmonic motion
`"m"("d"^2"x")/"dt"^2` = −kx ...........(1)
`("d"^2"x")/"dt"^2 = -"k"/"m""x"` .........(2)
Comparing the equation with simple harmonic motion equation, we get
`ω^2 = "k"/"m"` ........(3)
which means the angular frequency or natural frequency of the oscillator is
`ω = sqrt("k"/"m")` rad s−1 ..........(4)
The frequency of the oscillation is
f = `ω/(2π) = 1/(2π) sqrt("k"/"m")` Hertz ..........(5)
and the time period of the oscillation is
T = `1/"f" = 2π sqrt("m"/"k")` seconds .........(6)
APPEARS IN
संबंधित प्रश्न
Two bodies A and B whose masses are in the ratio 1 : 2 are suspended from two separate massless springs of force constants kA and kB respectively. If the two bodies oscillate vertically such that their maximum velocities are in the ratio 1 : 2, the ratio of the amplitude A to that of B is
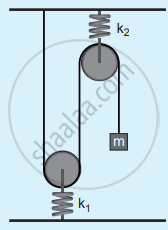
The time period for small vertical oscillations of block of mass m when the masses of the pulleys are negligible and spring constant k1 and k2 is
An ideal spring of spring constant k, is suspended from the ceiling of a room and a block of mass M is fastened to its lower end. If the block is released when the spring is un-stretched, then the maximum extension in the spring is
A pendulum is hung in a very high building oscillates to and fro motion freely like a simple harmonic oscillator. If the acceleration of the bob is 16 ms−2 at a distance of 4 m from the mean position, then the time period is
Write down the equation of the time period for the linear harmonic oscillator.
Discuss the simple pendulum in detail.
Describe the vertical oscillations of a spring.
Write short notes on the oscillations of the liquid column in the U-tube.
A piece of wood of mass m is floating erect in a liquid whose density is ρ. If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T = `2π sqrt("m"/("Ag"ρ))`
Compute the time period for the following system if the block of mass m is slightly displaced vertically down from its equilibrium position and then released. Assume that the pulley is light and smooth, strings and springs are light.