Advertisements
Advertisements
प्रश्न
Factorise the following:
a4 – 3a2 + 2
उत्तर
Let a2 = x
a4 – 3a2 + 2 = (a2)2 – 3a2 + 2
= x2 – 3x + 2
Product = 2 and sum = – 3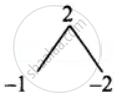
Split the middle term as – x and – 2x
x² – 3x + 2 = x2 – x – 2x + 2
= x(x – 1) – 2(x – 1)
= (x – 1)(x – 2)
a4 – 3a2 + 2 = (a2 – 1)(a2 – 2) ...[But a2 = x]
= (a + 1)(a – 1)(a2 – 2)
APPEARS IN
संबंधित प्रश्न
f(x) = 4x4 − 3x3 − 2x2 + x − 7, g(x) = x − 1
In the following two polynomials, find the value of a, if x + a is a factor x3 + ax2 − 2x +a + 4.
If \[x = \frac{1}{2}\] is a zero of the polynomial f(x) = 8x3 + ax2 − 4x + 2, find the value of a.
If x3 + 6x2 + 4x + k is exactly divisible by x + 2, then k =
Factorise the following:
12x2 + 36x2y + 27y2x2
Factorise the following:
(a + b)2 + 9(a + b) + 18
Factorise the following:
(p – q)2 – 6(p – q) – 16
Factorise the following:
m2 + 2mn – 24n2
Factorise:
x3 + x2 – 4x – 4
Factorise:
3x3 – x2 – 3x + 1
