Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by the curves y2 = 4x and 4x2 + 4y2 = 9 with x >= 0.
उत्तर

Required area is nothing but area bounded by the parabola y2 = 4x and the circle x2 + y2 = 9/4
To find the points of intersection.
Solving the given equations, we get
`x^2 + 4x - 9/4 = 0`
∴ 4x2 + 16x − 9 = 0
∴ 4x2 + 18x − 2x − 9 = 0
∴ (2x − 1)(2x + 9) = 0
∴ x = 1/2 or x = `-9/2` (not possible)
When x = 1/2 , y = `+- sqrt2`
∴ The curves intersect at `P(1/2, sqrt2) and Q(1/2, -sqrt2)`
Consider, y2 = 4x
∴ `y = 2x^(1/2) = y_1` ....(say)
Also, `x^2 + y^2 = 9/2`
`:. y^2 = 9/4 - x^2`
∴ y = `sqrt(9/4 - x^2) = y_2` ...(say)
∴ Required area = A(OPAQO) =2.A(OPAMO)
= 2[A(OPMO) + A(PAMP)]
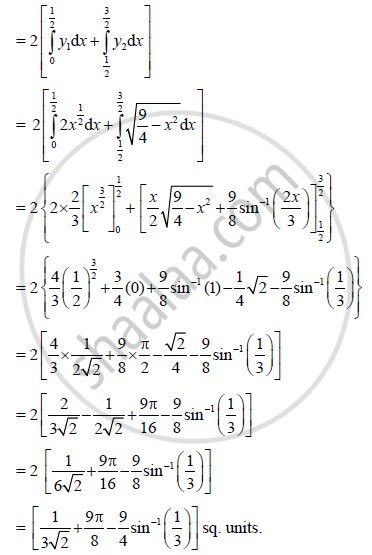
APPEARS IN
संबंधित प्रश्न
A body is heated at 110°C and placed in air at 10°C. After 1 hour its temperature is 60°C. How much additional time is required for it to cool to 35°C?
If the population of a country doubles in 60 years, in how many years will it be triple under
the assumption that the rate of increase in proportional to the number of inhabitants?
[Given : log 2 = 0.6912 and log 3 = 1.0986.]
Solve the differential equation `y - x dy/dx = 0`
