Advertisements
Advertisements
प्रश्न
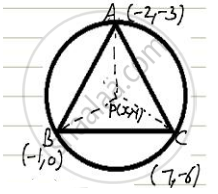
Find the circumcenter of the triangle whose vertices are (-2, -3), (-1, 0), (7, -6).
Advertisements
उत्तर
The circumference of a triangle is equidistance from the vertices of a triangle.
Let A(-2, -3), B(-1, 0) and C(7, -6) vertices of the given triangle and let P(x,y) be the circumference of this triangle, Then
PA = PB = PC
Now, PA = PB
`=> sqrt((-2-x)^2 + (-3 -y)^2) = sqrt((-1 - x)^2 + (0 - y)^2`
`=> 4 + x^2 + 4x + 9 + y^2 + 6y = 1 + x^2 + 2xz + y^2`
`=> 4 + x^2 + 4x + 9 + y^2 + 6y - 1 - x^2 - 2x - y^2 = 0`
`=> 2x + 6y + 12 = 0
=> 2(x + 3y + 6) = 0
=> x + 3y + 6 = 0 ... eq (1)
And PB = PC
`=> sqrt((-1-x)^2 + (0 - y)^2) = sqrt((7- x)^2 + (-6 - y)^2)`
Squaring both the sides
`=> (-1 - x)^2 + y^2 = (7 - x)^2 + (-6 -y)^2`
`=> 1 + x^2 + 2x + y^2 = (7 - x)^2 + (-6 - y)^2`
`=> 1 + x^2 + 2x + y^2 - 49 - x^2 + 14x - 36 - y^2 - 12y`
=> 16x - 12y - 84 = 0
`=> 4(4x - 3y - 21) = 0`
=> 4x - 3y - 21 = 0 ......eq(2)
Adding eq(1) and eq(2)
`=> x + 3y + 6 + 4x - 3y - 21 = 0`
=> x + 3y + 6 + 4x -3y - 21 = 0
=> 5x - 15 = 0
=> x = 15/5`
=> x = 3
putting the value of x in eq (2) and
we get
`=> 4 x 3 - 3y - 21 = 0`
`=> 12 - 3y - 21 = 0`
`=> -3y - 9 = 0`
`=> y = (-9)/3 = -3`
So the coordinates of the circumcentre P are (3, -3)
APPEARS IN
संबंधित प्रश्न
If P and Q are two points whose coordinates are (at2 ,2at) and (a/t2 , 2a/t) respectively and S is the point (a, 0). Show that `\frac{1}{SP}+\frac{1}{SQ}` is independent of t.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in the following figure. Champa and Chameli walk into the class and after observing for a few minutes, Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees.
Using distance formula, find which of them is correct.
Name the type of quadrilateral formed, if any, by the following point, and give reasons for your answer:
(−3, 5), (3, 1), (0, 3), (−1, −4)
Given a line segment AB joining the points A(–4, 6) and B(8, –3). Find
1) The ratio in which AB is divided by y-axis.
2) Find the coordinates of the point of intersection.
3) The length of AB.
Find the distance between the following pair of points:
(-6, 7) and (-1, -5)
The length of a line segment is of 10 units and the coordinates of one end-point are (2, -3). If the abscissa of the other end is 10, find the ordinate of the other end.
A(–8, 0), B(0, 16) and C(0, 0) are the vertices of a triangle ABC. Point P lies on AB and Q lies on AC such that AP : PB = 3 : 5 and AQ : QC = 3 : 5. Show that : PQ = `3/8` BC.
Find the distance between the points:
P(a + b, a - b) and Q(a - b, a + b)
Find x if distance between points L(x, 7) and M(1, 15) is 10.
Find the point on the x-axis equidistant from the points (5,4) and (-2,3).
Prove that the points (1 ,1),(-4 , 4) and (4 , 6) are the certices of an isosceles triangle.
Prove taht the points (-2 , 1) , (-1 , 4) and (0 , 3) are the vertices of a right - angled triangle.
Find the distance of the following points from origin.
(a cos θ, a sin θ).
Find distance CD where C(– 3a, a), D(a, – 2a)
The distance between the points A(0, 6) and B(0, -2) is ______.
If the distance between the points (4, P) and (1, 0) is 5, then the value of p is ______.
Find the value of a, if the distance between the points A(–3, –14) and B(a, –5) is 9 units.
|
In a GPS, The lines that run east-west are known as lines of latitude, and the lines running north-south are known as lines of longitude. The latitude and the longitude of a place are its coordinates and the distance formula is used to find the distance between two places. The distance between two parallel lines is approximately 150 km. A family from Uttar Pradesh planned a round trip from Lucknow (L) to Puri (P) via Bhuj (B) and Nashik (N) as shown in the given figure below.
|
Based on the above information answer the following questions using the coordinate geometry.
- Find the distance between Lucknow (L) to Bhuj (B).
- If Kota (K), internally divide the line segment joining Lucknow (L) to Bhuj (B) into 3 : 2 then find the coordinate of Kota (K).
- Name the type of triangle formed by the places Lucknow (L), Nashik (N) and Puri (P)
[OR]
Find a place (point) on the longitude (y-axis) which is equidistant from the points Lucknow (L) and Puri (P).
The distance between the points (0, 5) and (–3, 1) is ______.
