Advertisements
Advertisements
प्रश्न
Find out the outward flux to a point charge +q placed at the centre of a cube of side ‘a’. Why is it found to be independent of the size and shape of the surface enclosing it? Explain.
उत्तर
Let a cube of side a enclose charge +q at its centre.
Because the electric flux through the square surface is `phi=q/(6in_0)`the square surfaces of cube are six. Hence, according to Gauss’s theorem in electrostatics, the total outward flux due to a charge +q of a cube is
`phi=6xx(q/(6in_0))=q/in_0`
The result shows that the electric flux passing through a closed surface is proportional to the charge enclosed. In addition, the result reinforces that the flux is independent of the shape and size of the closed surface.
APPEARS IN
संबंधित प्रश्न
What is the electric flux through a cube of side 1 cm which encloses an electric dipole?
Given the electric field in the region `vecE=2xhati`, find the net electric flux through the cube and the charge enclosed by it.
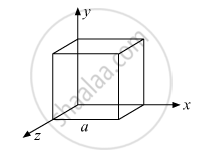
Given a uniform electric field `vecE=5xx10^3hati`N/C, find the flux of this field through a square of 10 cm on a side whose plane is parallel to the y-z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis ?
What is the net flux of the uniform electric field of previous question through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC/m2.
- Find the charge on the sphere.
- What is the total electric flux leaving the surface of the sphere?
Define Electric Flux. Write its SI unit.
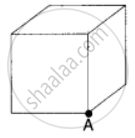
The total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is ______.
The S.I. unit of electric flux is ______
A hollow sphere of radius R has a point charge q at its centre. Electric flux emanating from the sphere is X. How will the electric flux change, if at all, when charge q is replaced by an electric dipole?
