Advertisements
Advertisements
प्रश्न
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC/m2.
- Find the charge on the sphere.
- What is the total electric flux leaving the surface of the sphere?
उत्तर
R = `2.4/2 "m"` = 1.2 m,
σ = 80.0 μ /c m-2
= 80 × 10-6 C m-2
- As σ = `q/(4pi"R"^2)`
so, q = 4πR2 × σ
= 4 × 3.14 ×(1.22) × 80 ×10-6
or q = 1.45 × 10-3 C - Φ = `q/ε_0`
= `(1.45 xx 10^-3)/(8.85 xx 10^-12)`
= 1.64 × 108 N m2 C-1
APPEARS IN
संबंधित प्रश्न
"The outward electric flux due to charge +Q is independent of the shape and size of the surface which encloses is." Give two reasons to justify this statement.
What is the electric flux through a cube of side 1 cm which encloses an electric dipole?
Consider a uniform electric field E = 3 × 103 `bbhat i` N/C.
- What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?
- What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
What is the net flux of the uniform electric field of previous question through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Define Electric Flux. Write its SI unit.
Two charges of magnitudes −2Q and +Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its centre at the origin?
A thin straight infinitely long conducting wire having charge density λ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
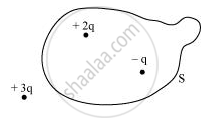
Figure shows three point charges +2q, −q and + 3q. Two charges + 2q and −q are enclosed within a surface ‘S’. What is the electric flux due to this configuration through the surface ‘S’?
Mark the correct options:
The following figure shows a closed surface that intersects a conducting sphere. If a positive charge is placed at point P, the flux of the electric field through the closed surface

The electric field in a region is given by `vec"E"` = 5 `hatk`N/C. Calculate the electric flux Through a square of side 10.0 cm in the following cases
- The square is along the XY plane
- The square is along XZ plane
- The normal to the square makes an angle of 45° with the Z axis.
A uniform electric field of intensity 400 N/C, exists in a certain region. How much flux will cross a given area of 10 cm2 in this region, if the area vector is inclined at 60° to the direction of the field?
A charge 'Q' µC is placed at the centre of a cube. The flux through one face and two opposite faces of the cube is respectively ______.
A charged particle q is placed at the centre O of cube of length L (A B C D E F G H). Another same charge q is placed at a distance L from O. Then the electric flux through ABCD is ______.
What will be the total flux through the faces of the cube (figure) with side of length a if a charge q is placed at

- A: a corner of the cube.
- B: mid-point of an edge of the cube.
- C: centre of a face of the cube.
- D: mid-point of B and C.
The electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 20 V-m. The flux over a concentric sphere of radius 20 cm will be ______.
A hollow sphere of radius R has a point charge q at its centre. Electric flux emanating from the sphere is X. How will the electric flux change, if at all, when charge q is replaced by an electric dipole?
