Advertisements
Advertisements
प्रश्न
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC/m2.
- Find the charge on the sphere.
- What is the total electric flux leaving the surface of the sphere?
उत्तर
R = `2.4/2 "m"` = 1.2 m,
σ = 80.0 μ /c m-2
= 80 × 10-6 C m-2
- As σ = `q/(4pi"R"^2)`
so, q = 4πR2 × σ
= 4 × 3.14 ×(1.22) × 80 ×10-6
or q = 1.45 × 10-3 C - Φ = `q/ε_0`
= `(1.45 xx 10^-3)/(8.85 xx 10^-12)`
= 1.64 × 108 N m2 C-1
APPEARS IN
संबंधित प्रश्न
Define electric flux.
Write its (electric flux.) S.I unit.
Given the electric field in the region `vecE=2xhati`, find the net electric flux through the cube and the charge enclosed by it.
Two charges of magnitudes −2Q and +Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its centre at the origin?
A thin straight infinitely long conducting wire having charge density λ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
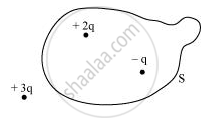
Figure shows three point charges +2q, −q and + 3q. Two charges + 2q and −q are enclosed within a surface ‘S’. What is the electric flux due to this configuration through the surface ‘S’?
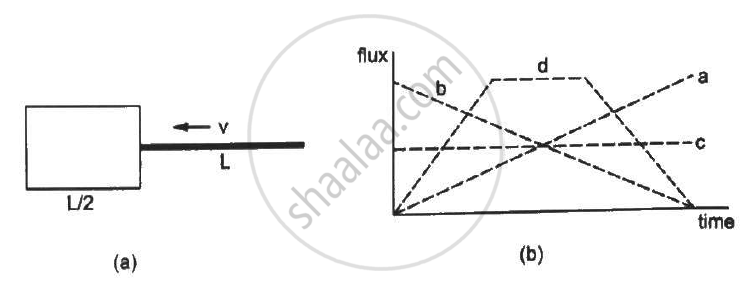
Following Figure (a) shows an imaginary cube of edge L/2. A uniformly charged rod of length (L) moves towards the left at a small but constant speed `nu.` At t = 0, the left end just touches the centre of the face of the cube opposite it. Which of the graphs shown in the figure (b) represents the flux of the electric field through the cube as the rod goes through it?
If the flux of the electric field through a closed surface is zero,
(a) the electric field must be zero everywhere on the surface
(b) the electric field may be zero everywhere on the surface
(c) the charge inside the surface must be zero
(d) the charge in the vicinity of the surface must be zero
The following figure shows a closed surface that intersects a conducting sphere. If a positive charge is placed at point P, the flux of the electric field through the closed surface

If the flux associated with a coil changes at the rate of 360 webers every 4 minutes, then the induced e.m.f. is ______
A charge 'Q' µC is placed at the centre of a cube. The flux through one face and two opposite faces of the cube is respectively ______.
The SI unit of electric flux is ______.
An electric charge q is placed at the centre of a cube of side a. The electric flux on one of its faces will be ______.
The S.I. unit of electric flux is ______
A hollow sphere of radius R has a point charge Q at its centre. Electric flux emanating from it is `phi`. If both the charge and the radius of the sphere are doubled, electric flux emanating from the sphere will ______.
A hollow sphere of radius R has a point charge q at its centre. Electric flux emanating from the sphere is X. How will the electric flux change, if at all, when charge q is replaced by an electric dipole?
