Advertisements
Advertisements
प्रश्न
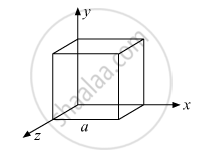
Given the electric field in the region `vecE=2xhati`, find the net electric flux through the cube and the charge enclosed by it.
उत्तर
Since the electric field has only x component, for faces normal to x direction, the angle between E and ∆S is ±π/2. Therefore, the flux is separately zero for each face of the cube except the two shaded ones.
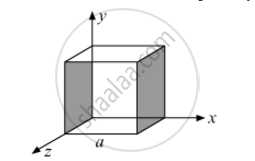
The magnitude of the electric field at the left face is EL = 0 (As x = 0 at the left face)
The magnitude of the electric field at the right face is ER = 2a (As x = a at the right face)
The corresponding fluxes are
`phi_L=vecE.DeltavecS=0`
`phi_R=vecE_R.DeltavecS=E_RDeltaScostheta=E_RDeltaS " "(.:theta=0^@)`
⇒ϕR= ERa2
Net flux (ϕ) through the cube = ϕL+ϕR=0+ERa2=ERa2
ϕ=2a(a)2=2a3
We can use Gauss’s law to find the total charge q inside the cube.
`phi=q/(epsilon_0)`
q=ϕε0=2a3ε0
APPEARS IN
संबंधित प्रश्न
"The outward electric flux due to charge +Q is independent of the shape and size of the surface which encloses is." Give two reasons to justify this statement.
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 103 N m2/C.
- What is the net charge inside the box?
- If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?
Given a uniform electric field \[\vec{E} = 2 \times {10}^3 \ \hat{i}\] N/C, find the flux of this field through a square of side 20 cm, whose plane is parallel to the y−z plane. What would be the flux through the same square, if the plane makes an angle of 30° with the x−axis ?
Two charges of magnitudes +4Q and − Q are located at points (a, 0) and (− 3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘2a’ with its centre at the origin?
A circular ring of radius r made of a non-conducting material is placed with its axis parallel to a uniform electric field. The ring is rotated about a diameter through 180°. Does the flux of the electric field change? If yes, does it decrease or increase?
It is said that any charge given to a conductor comes to its surface. Should all the protons come to the surface? Should all the electrons come to the surface? Should all the free electrons come to the surface?
Electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 25 V m. The flux over a concentric sphere of radius 20 cm will be _____________ .
The electric field in a region is given by `vec"E"` = 5 `hatk`N/C. Calculate the electric flux Through a square of side 10.0 cm in the following cases
- The square is along the XY plane
- The square is along XZ plane
- The normal to the square makes an angle of 45° with the Z axis.
The S.I. unit of electric flux is ______
A circular disc of radius 'r' is placed along the plane of paper. A uniform electric field `vec"E"` is also present in the plane of paper. What amount of electric flux is associated with it?