Advertisements
Advertisements
प्रश्न
Two charges of magnitudes +4Q and − Q are located at points (a, 0) and (− 3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘2a’ with its centre at the origin?
उत्तर
Gauss’ theorem states that the electric flux through a closed surface enclosing a charge is equal to `1/epsi_0`times the magnitude of the charge enclosed.
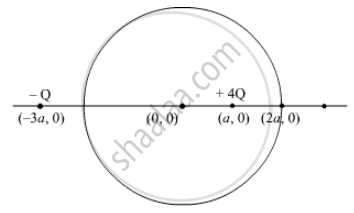
The sphere enclose charge = +4Q.
Thus,`phi = (4Q)/epsi_0`
APPEARS IN
संबंधित प्रश्न
How does the electric flux due to a point charge enclosed by a spherical Gaussian surface get affected when its radius is increased?
Define electric flux.
Write its (electric flux.) S.I unit.
What is the electric flux through a cube of side 1 cm which encloses an electric dipole?
Given a uniform electric filed \[\vec{E} = 4 \times {10}^3 \ \hat{i} N/C\]. Find the flux of this field through a square of 5 cm on a side whose plane is parallel to the Y-Z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis?
Mark the correct options:
A charge 'Q' µC is placed at the centre of a cube. The flux through one face and two opposite faces of the cube is respectively ______.
The electric field intensity due to an infinite cylinder of radius R and having charge q per unit length at a distance rir r(r > R) from its axis is ______.
An electric charge q is placed at the center of a cube of side ℓ. The electric flux on one of its faces will be ______.
A hollow sphere of radius R has a point charge q at its centre. Electric flux emanating from the sphere is X. How will the electric flux change, if at all, when radius of the sphere is doubled?
