Advertisements
Advertisements
प्रश्न
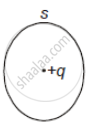
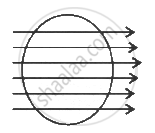
The following figure shows a closed surface that intersects a conducting sphere. If a positive charge is placed at point P, the flux of the electric field through the closed surface

विकल्प
will remain zero
will become positive
will become negative
will become undefined
उत्तर
will become positive
A positive charge at point P will induce a negative charge on the near face of the conducting sphere, whereas the positive charge on the farther end of the sphere. As this father end is enclosed or intersected by the closed surface, so the flux through it will become positive due to the induced positive charge.
APPEARS IN
संबंधित प्रश्न
Define electric flux.
Find out the outward flux to a point charge +q placed at the centre of a cube of side ‘a’. Why is it found to be independent of the size and shape of the surface enclosing it? Explain.
Define Electric Flux. Write its SI unit.
A thin straight infinitely long conducting wire having charge density λ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
A small plane area is rotated in an electric field. In which orientation of the area, is the flux of the electric field through the area maximum? In which orientation is it zero?
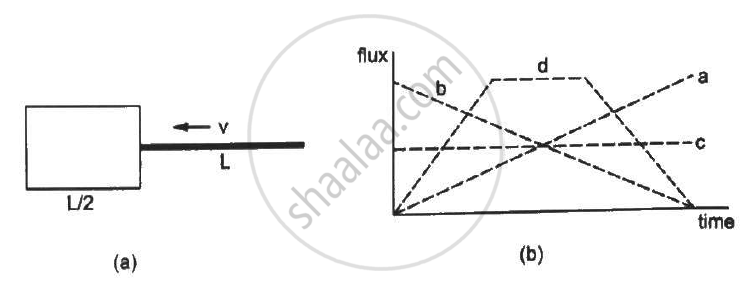
Following Figure (a) shows an imaginary cube of edge L/2. A uniformly charged rod of length (L) moves towards the left at a small but constant speed `nu.` At t = 0, the left end just touches the centre of the face of the cube opposite it. Which of the graphs shown in the figure (b) represents the flux of the electric field through the cube as the rod goes through it?
A uniform electric field of intensity 400 N/C, exists in a certain region. How much flux will cross a given area of 10 cm2 in this region, if the area vector is inclined at 60° to the direction of the field?
The electric flux through the surface ______.
 |
 |
 |
 |
| (i) | (ii) | (iii) | (iv) |
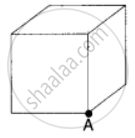
The total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is ______.
A cylinder of radius R and length L is placed in a uniform electric field E parallel to the cylinder axis. The total flux for the surface of the cylinder is given by ______.
Total electric flux coming out of a unit positive charge kept in air is ______.
A point charge q is placed at a distance a/2 directly above the centre of a square of side a. The electric flux through the square is ______.
The electric field in a region is given by `bar"E" = 4hat"i" + 10hat"j"` N/C. The flux of this field through a square of 10 cm on a side whose plane is parallel to the XZ plane.
A circular disc of radius 'r' is placed along the plane of paper. A uniform electric field `vec"E"` is also present in the plane of paper. What amount of electric flux is associated with it?
What will be the total flux through the faces of the cube (figure) with side of length a if a charge q is placed at

- A: a corner of the cube.
- B: mid-point of an edge of the cube.
- C: centre of a face of the cube.
- D: mid-point of B and C.
The electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 20 V-m. The flux over a concentric sphere of radius 20 cm will be ______.
A hollow sphere of radius R has a point charge q at its centre. Electric flux emanating from the sphere is X. How will the electric flux change, if at all, when radius of the sphere is doubled?
