Advertisements
Advertisements
प्रश्न
A thin straight infinitely long conducting wire having charge density λ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
उत्तर
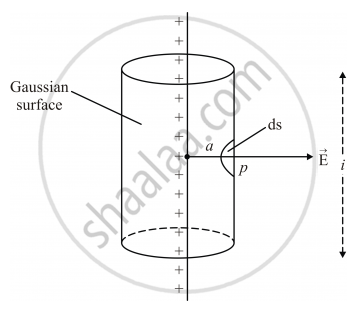
The thin infinitely long straight line has a linear charge density λ.
Since the electric field for this kind of configuration will be radial and perpendicular to the wire, there will be no flux through the flat surfaces of the cylinder. Also, the electric field (E) will be constant at every point on the curved surface of the cylinder (as all points on it are equidistant from the wire) and perpendicular to it.
We shall us Gauss's law to find the electric flux through the cylinder. The charge enclosed by the cylinder is λ × l, as l is the length of the cylinder and it is also the length of the charged wire within the cylinder.
We know,
`\text { Electric flux} = (\text { Charge enclosed})/epsi_0 = (lambdal)/epsi_0`
APPEARS IN
संबंधित प्रश्न
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC/m2.
- Find the charge on the sphere.
- What is the total electric flux leaving the surface of the sphere?
Two charges of magnitudes −3Q and + 2Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘5a’ with its centre at the origin?
It is said that any charge given to a conductor comes to its surface. Should all the protons come to the surface? Should all the electrons come to the surface? Should all the free electrons come to the surface?
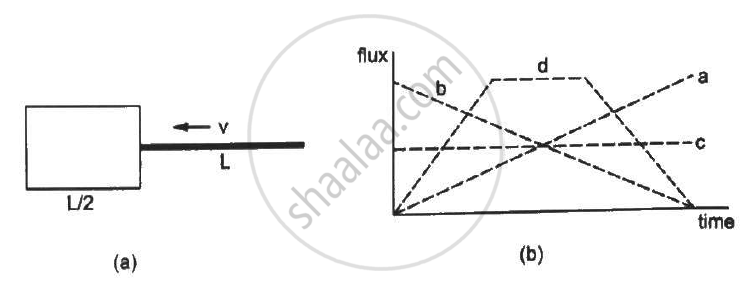
Following Figure (a) shows an imaginary cube of edge L/2. A uniformly charged rod of length (L) moves towards the left at a small but constant speed `nu.` At t = 0, the left end just touches the centre of the face of the cube opposite it. Which of the graphs shown in the figure (b) represents the flux of the electric field through the cube as the rod goes through it?
A charge q is placed at the centre of the open end of a cylindrical vessel (see the figure). The flux of the electric field through the surface of the vessel is ____________ .

If the flux associated with a coil changes at the rate of 360 webers every 4 minutes, then the induced e.m.f. is ______
If the electric flux entering and leaving an enclosed surface respectively is Φ1 and Φ2, the electric charge inside the surface will be
A charge Qµc is placed at the centre of a cube the flux coming from any surface will be.
The electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 20 V-m. The flux over a concentric sphere of radius 20 cm will be ______.
A hollow sphere of radius R has a point charge q at its centre. Electric flux emanating from the sphere is X. How will the electric flux change, if at all, when radius of the sphere is doubled?
