Advertisements
Advertisements
Question
A thin straight infinitely long conducting wire having charge density λ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
Solution
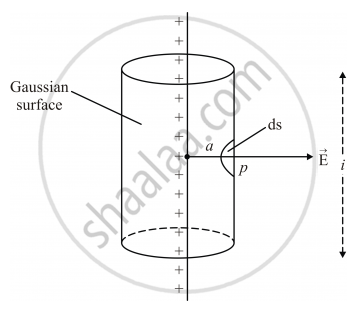
The thin infinitely long straight line has a linear charge density λ.
Since the electric field for this kind of configuration will be radial and perpendicular to the wire, there will be no flux through the flat surfaces of the cylinder. Also, the electric field (E) will be constant at every point on the curved surface of the cylinder (as all points on it are equidistant from the wire) and perpendicular to it.
We shall us Gauss's law to find the electric flux through the cylinder. The charge enclosed by the cylinder is λ × l, as l is the length of the cylinder and it is also the length of the charged wire within the cylinder.
We know,
`\text { Electric flux} = (\text { Charge enclosed})/epsi_0 = (lambdal)/epsi_0`
APPEARS IN
RELATED QUESTIONS
How does the electric flux due to a point charge enclosed by a spherical Gaussian surface get affected when its radius is increased?
What is the electric flux through a cube of side 1 cm which encloses an electric dipole?
Given a uniform electric filed \[\vec{E} = 4 \times {10}^3 \ \hat{i} N/C\]. Find the flux of this field through a square of 5 cm on a side whose plane is parallel to the Y-Z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis?
A circular ring of radius r made of a non-conducting material is placed with its axis parallel to a uniform electric field. The ring is rotated about a diameter through 180°. Does the flux of the electric field change? If yes, does it decrease or increase?
The SI unit of electric flux is ______.
A cylinder of radius R and length L is placed in a uniform electric field E parallel to the cylinder axis. The total flux for the surface of the cylinder is given by ______.
The S.I. unit of electric flux is ______
The electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 20 V-m. The flux over a concentric sphere of radius 20 cm will be ______.
