Advertisements
Advertisements
प्रश्न
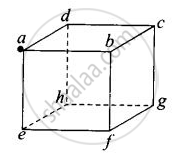
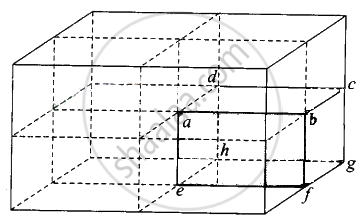
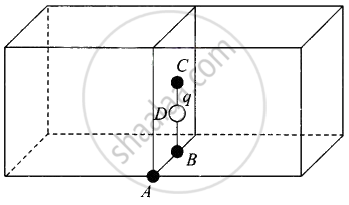
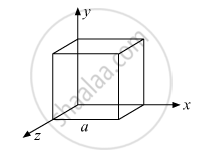
What will be the total flux through the faces of the cube (figure) with side of length a if a charge q is placed at

- A: a corner of the cube.
- B: mid-point of an edge of the cube.
- C: centre of a face of the cube.
- D: mid-point of B and C.
उत्तर
a. Use of symmetry consideration may be useful in problems of flux calculation. We can imagine the charged particle is placed at the centre of a cube of side 2a. We can observe that the charge is being shared equally by 8 cubes. Therefore, total flux through the faces of the given cube = `q/(8ε_0)`
 |
 |
| (A) | (B) |
b. If the charge q is placed at B, middle point of an edge of the cube, it is shared equally by 4 cubes. Therefore, total flux through the faces of the given cube = `q/(4ε_0)`
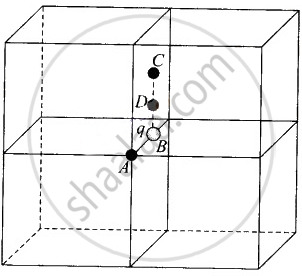
c. If the charge q is placed at C, the centre of a face of the cube, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the given cube = `q/(2ε_0)`
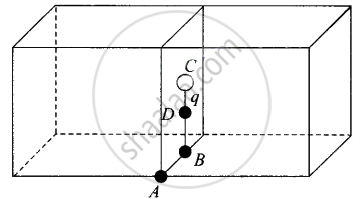
d. Finally, if charge q is placed at D, the mid-point of B and C, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the
given cube = `q/(2ε_0)`
APPEARS IN
संबंधित प्रश्न
"The outward electric flux due to charge +Q is independent of the shape and size of the surface which encloses is." Give two reasons to justify this statement.
Given the electric field in the region `vecE=2xhati`, find the net electric flux through the cube and the charge enclosed by it.
Consider a uniform electric field E = 3 × 103 `bbhat i` N/C.
- What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?
- What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
A thin straight infinitely long conducting wire having charge density λ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
Choose the correct answer from given options
The electric flux through a closed Gaussian surface depends upon
A charge 'Q' µC is placed at the centre of a cube. The flux through one face and two opposite faces of the cube is respectively ______.
A charged particle q is placed at the centre O of cube of length L (A B C D E F G H). Another same charge q is placed at a distance L from O. Then the electric flux through ABCD is ______.
The electric field in a region is given by `bar"E" = 4hat"i" + 10hat"j"` N/C. The flux of this field through a square of 10 cm on a side whose plane is parallel to the XZ plane.
In a region of space having a uniform electric field E, a hemispherical bowl of radius r is placed. The electric flux Φ through the bowl is:
A hollow sphere of radius R has a point charge q at its centre. Electric flux emanating from the sphere is X. How will the electric flux change, if at all, when radius of the sphere is doubled?
