Advertisements
Advertisements
Question
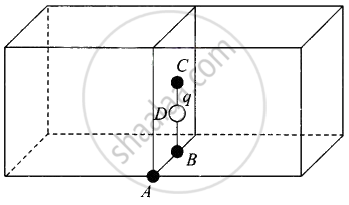
What will be the total flux through the faces of the cube (figure) with side of length a if a charge q is placed at

- A: a corner of the cube.
- B: mid-point of an edge of the cube.
- C: centre of a face of the cube.
- D: mid-point of B and C.
Solution
a. Use of symmetry consideration may be useful in problems of flux calculation. We can imagine the charged particle is placed at the centre of a cube of side 2a. We can observe that the charge is being shared equally by 8 cubes. Therefore, total flux through the faces of the given cube = `q/(8ε_0)`
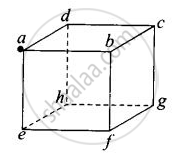 |
 |
| (A) | (B) |
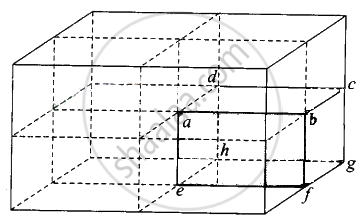
b. If the charge q is placed at B, middle point of an edge of the cube, it is shared equally by 4 cubes. Therefore, total flux through the faces of the given cube = `q/(4ε_0)`
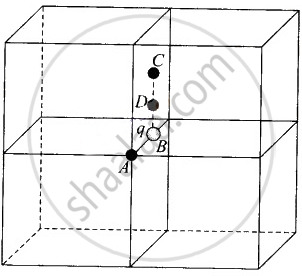
c. If the charge q is placed at C, the centre of a face of the cube, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the given cube = `q/(2ε_0)`
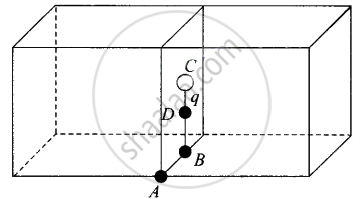
d. Finally, if charge q is placed at D, the mid-point of B and C, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the
given cube = `q/(2ε_0)`
APPEARS IN
RELATED QUESTIONS
How does the electric flux due to a point charge enclosed by a spherical Gaussian surface get affected when its radius is increased?
Given a uniform electric field `vecE=5xx10^3hati`N/C, find the flux of this field through a square of 10 cm on a side whose plane is parallel to the y-z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis ?
Given a uniform electric filed \[\vec{E} = 4 \times {10}^3 \ \hat{i} N/C\]. Find the flux of this field through a square of 5 cm on a side whose plane is parallel to the Y-Z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis?
Two charges of magnitudes −3Q and + 2Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘5a’ with its centre at the origin?
Two charges of magnitudes +4Q and − Q are located at points (a, 0) and (− 3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘2a’ with its centre at the origin?
A small plane area is rotated in an electric field. In which orientation of the area, is the flux of the electric field through the area maximum? In which orientation is it zero?
If the flux associated with a coil changes at the rate of 360 webers every 4 minutes, then the induced e.m.f. is ______
A charge 'Q' µC is placed at the centre of a cube. The flux through one face and two opposite faces of the cube is respectively ______.
The SI unit of electric flux is ______.
The electric field in a region is given by `bar"E" = 4hat"i" + 10hat"j"` N/C. The flux of this field through a square of 10 cm on a side whose plane is parallel to the XZ plane.
