Advertisements
Advertisements
Question
Two charges of magnitudes −3Q and + 2Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘5a’ with its centre at the origin?
Solution
Gauss’ theorem states that the electric flux through a closed surface enclosing a charge is equal to `1/epsi_0`times the magnitude of the charge enclosed.
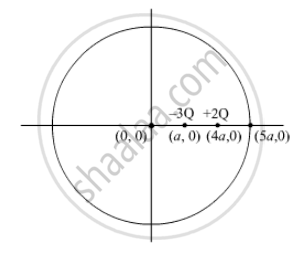
The sphere enclose charge = -3Q + 2Q = -Q
Therefore, `phi= Q/epsi_0`
APPEARS IN
RELATED QUESTIONS
Write its (electric flux.) S.I unit.
Find out the outward flux to a point charge +q placed at the centre of a cube of side ‘a’. Why is it found to be independent of the size and shape of the surface enclosing it? Explain.
Given a uniform electric field `vecE=5xx10^3hati`N/C, find the flux of this field through a square of 10 cm on a side whose plane is parallel to the y-z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis ?
Define Electric Flux. Write its SI unit.
Two charges of magnitudes +4Q and − Q are located at points (a, 0) and (− 3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘2a’ with its centre at the origin?
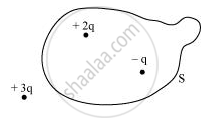
Figure shows three point charges +2q, −q and + 3q. Two charges + 2q and −q are enclosed within a surface ‘S’. What is the electric flux due to this configuration through the surface ‘S’?
The total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is ______.
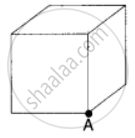
What will be the total flux through the faces of the cube (figure) with side of length a if a charge q is placed at

- A: a corner of the cube.
- B: mid-point of an edge of the cube.
- C: centre of a face of the cube.
- D: mid-point of B and C.
A hollow sphere of radius R has a point charge q at its centre. Electric flux emanating from the sphere is X. How will the electric flux change, if at all, when radius of the sphere is doubled?
