Advertisements
Advertisements
प्रश्न
Two charges of magnitudes −3Q and + 2Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘5a’ with its centre at the origin?
उत्तर
Gauss’ theorem states that the electric flux through a closed surface enclosing a charge is equal to `1/epsi_0`times the magnitude of the charge enclosed.
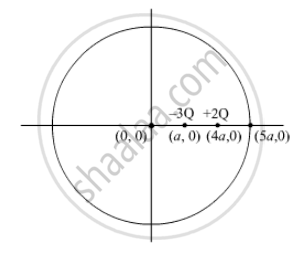
The sphere enclose charge = -3Q + 2Q = -Q
Therefore, `phi= Q/epsi_0`
APPEARS IN
संबंधित प्रश्न
How does the electric flux due to a point charge enclosed by a spherical Gaussian surface get affected when its radius is increased?
What is the electric flux through a cube of side 1 cm which encloses an electric dipole?
Given the electric field in the region `vecE=2xhati`, find the net electric flux through the cube and the charge enclosed by it.
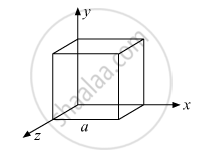
What is the net flux of the uniform electric field of previous question through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
A small plane area is rotated in an electric field. In which orientation of the area, is the flux of the electric field through the area maximum? In which orientation is it zero?
A circular ring of radius r made of a non-conducting material is placed with its axis parallel to a uniform electric field. The ring is rotated about a diameter through 180°. Does the flux of the electric field change? If yes, does it decrease or increase?
It is said that any charge given to a conductor comes to its surface. Should all the protons come to the surface? Should all the electrons come to the surface? Should all the free electrons come to the surface?
Choose the correct answer from given options
The electric flux through a closed Gaussian surface depends upon
The electric field in a region is given by `vec"E"` = 5 `hatk`N/C. Calculate the electric flux Through a square of side 10.0 cm in the following cases
- The square is along the XY plane
- The square is along XZ plane
- The normal to the square makes an angle of 45° with the Z axis.
